
| 慧慧 | 116 | 124 | 130 | 126 | 121 | 127 | 126 | 122 | 125 | 123 |
| 聪聪 | 122 | 124 | 125 | 128 | 119 | 120 | 121 | 128 | 114 | 119 |
分析 (1)把慧慧和聪聪的成绩都减去125,然后计算她们的平均成绩;
(2)根据方差公式计算两组数据的方差;
(3)根据平均数的大小和方差的意义进行判断;
(4)画树状图展示所有6种等可能的结果数,再找出两名学生分别在初三•二班和初三•三班的结果数,然后根据概率公式计算.
解答 解:(1)慧慧的平均分数=125+$\frac{1}{10}$(-9-1+5+1+6+2+1-3+0-2)=125(分),
聪聪的平均分数=125+$\frac{1}{10}$(-3-1+0+3-6-5+6+3-11-6)=123(分);
(2)慧慧成绩的方差 S2=$\frac{1}{10}$[92+12+52+12+42+22+12+32+02+22]=14.2,
聪聪成绩的方差S2=$\frac{1}{10}$[12+12+22+52+42+32+82+52+92+42]=24.2,
(3)根据(1)可知慧慧的平均成绩要好于聪聪,根据(2)可知慧慧的方差小于聪聪的方差,因为方差越小越稳定,所以慧慧的成绩比聪聪的稳定,因此选慧慧参加全国数学竞赛更合适一些.
(4)画树状图为: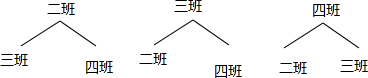
共有6种等可能的结果数,其中两名学生分别在初三•二班和初三•三班的结果数为2,
所以两名学生分别在初三•二班和初三•三班的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了平均数的计算方法和方差的计算.


科目:初中数学 来源: 题型:解答题
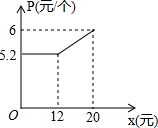 某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.
某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32017-1 | B. | 32018-1 | C. | $\frac{{3}^{2017}-1}{4}$ | D. | $\frac{{3}^{2017}-1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com