
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C在数轴上表示的数是10,若线段 AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的数度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 ;(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式 BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
【答案】(1)-6+6t,10+2t;(2)运动3秒或5秒后BC=4;(3)存在关系式BD﹣AP=3PC,此时PD=5.
【解析】
(1)根据数轴上的两点之间距离公式即可求出答案;
(2)设运动ts后,根据BC=4,分点B在点C的左、右两侧两种情况,列出方程即可求出t的值;
(3)假设存在点P,使BD﹣AP=3PC.设BD=x,则CB=4-x,AC=2-(4-x)=x-2,根据题意可知点P只能在C点左侧,得出AP+CP=AC,再结合BD﹣AP=3PC可求得PC的长,从而可求出此时PD的长.
解:(1)AB=2,CD=4,点A在数轴上表示的数是﹣8,点C在数轴上表示的数是10,
∴未运动之前,点B表示的数为-6,点D表示的数为14,
∴向右运动t秒后,点B,点C表示的数分别为-6+6t,10+2t.
故答案为:-6+6t,10+2t;
(2)设运动t秒后,BC=4,由题意可知:
当点B在点C左侧时,
∴(10+2t)-(-6+6t)=4,解得t=3;
当点B在点C的右侧时,
或(-6+6t)-(10+2t)=4,解得t=5,
答:运动3秒或5秒后BC=4;
(3)存在关系式BD-AP=3PC.理由如下:
设BD=x,则CB=4-x,AC=2-(4-x)=x-2,
∵点B运动到线段CD上,点P不在线段CD上,如图,点P只能在点C的左侧,
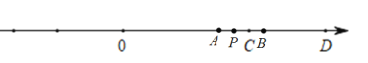
∴AP+CP=AC,
∵BD-AP=3PC,
∴BD=x=AP+PC+2PC=AC+2PC=x-2+2PC,
∴PC=1,
∴当PC=1时,BD-AP=3PC,
即PD=PC+CD=1+4=5.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】在复习课上,wsy老师要求写出几个与实数有关的结论:小明同学写了以下5个:
①任何无理数都是无限不循环小数;
②有理数与数轴上的点一一对应;
③在1和3之间的无理数有且只有![]() 这5个;
这5个;
④![]() 是分数,它是有理数;
是分数,它是有理数;
⑤由四舍五入得到的近似数7.30表示大于或等于7.295,而小于7.305的数.其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
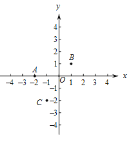
例如:点![]() (
(![]() ,0) ,点
,0) ,点 ![]() (1,1) ,点
(1,1) ,点 ![]() (
(![]() ,
, ![]() ),则
),则![]() 、
、![]() 、
、![]() 三点的 “横长”
三点的 “横长”![]() =|
=|![]() |=3,
|=3,![]() 、
、![]() 、
、![]() 三点的“纵长”
三点的“纵长”![]() =|
=|![]() |=3. 因为
|=3. 因为![]() =
=![]() ,所以
,所以![]() 、
、![]() 、
、![]() 三点为正方点.
三点为正方点.
(1)在点![]() (3,5) ,
(3,5) ,![]() (3,
(3,![]() ) ,
) ,![]() (
(![]() ,
,![]() )中,与点
)中,与点![]() 、
、![]() 为正方点的是 ;
为正方点的是 ;
(2)点P (0,t)为![]() 轴上一动点,若
轴上一动点,若![]() ,
,![]() ,
,![]() 三点为正方点,
三点为正方点,![]() 的值为 ;
的值为 ;
(3)已知点![]() (1,0).
(1,0).
①平面直角坐标系中的点![]() 满足以下条件:点
满足以下条件:点![]() ,
,![]() ,
,![]() 三点为正方点,在图中画出所有符合条件的点
三点为正方点,在图中画出所有符合条件的点![]() 组成的图形;
组成的图形;
②若直线![]() :
:![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 三点为正方点,直接写出m的取值范围.
三点为正方点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
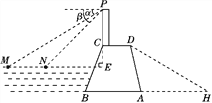
【题目】某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米).
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1∶0.25.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1∶1.75.施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备.工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan 31°≈0.60,sin 31°≈0.52)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在平面直角坐标系中,抛物线y=x![]() +5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
+5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
(1)求点A、B、C的坐标;
(2)求抛物线y=x![]() +5x+4关于坐标原点O对称的抛物线的函数表达式;
+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为![]() ,与x轴交于
,与x轴交于![]() 、
、![]() 两点,与y轴交于
两点,与y轴交于![]() 点,在以A、B、C、M、
点,在以A、B、C、M、![]() 、
、![]() 、
、![]() 、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
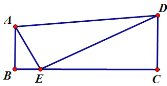
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°
(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE
(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
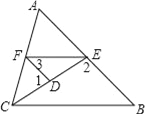
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com