练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，AB=AC，∠BAC=30°．点D为△ABC内一点，且DB=DC，∠DCB=30°．点E为BD延长线上一点，且AE=AB．

    (1)求∠ADE的度数；

    (2)若点M在DE上，且DM=DA，求证：ME=DC．


    60°；略．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    平面直角坐标系中点M(a，－2)和点N(3，b)关于y轴对称，则a+b=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果一个正数m的两个平方根分别是2a－3和a－9，求2m－2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若是的整数部分，是16的平方根，且，求的算术平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    (1)阅读理解：

    我们知道，只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角，但是这个任务可以借助如图所示的一边上有刻度的勾尺完成，勾尺的直角顶点为P，“宽臂”的宽度=PQ=QR=RS，(这个条件很重要哦！)勾尺的一边MN满足M，N，Q三点共线(所以PQ⊥MN)．

    下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程：

    第一步：画直线DE使DE//BC，且这两条平行线的距离等于PQ；

    第二步：移动勾尺到合适位置，使其顶点P落在DE上，使勾尺的MN边经过点B，同时让点R落在∠ABC的BA边上；

    第三步：标记此时点Q和点P所在位置，作射线BQ和射线BP．

    请完成第三步操作，图中的三等分线是射线____、____．

    (2)在(1)的条件下完成三等分∠ABC的证明过程：

    (3)在(1)的条件下探究：

    是否成立？如果成立，请说明理由；如果不成立，请在下图中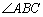的外部画出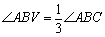(无需写画法，保留画图痕迹即可)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，D为∠BAC的外角平分线上一点并且满足BD=CD，∠DBC=∠DCB，过D作DE⊥AC于E，DF⊥AB交BA的延长线于F，则下列结论：①△CDE≌△BDF；②CE=AB+AE；③∠DBF=∠DCE；④∠DAE=∠DAF．其中正确的结论有(　　)

    A．1个          B．2个          C．3个          D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列一元二次方程有两个不等的实数根的是

      A.（n－25）2＝0                         B.y2＋1＝0    

      C.x2＋3x－5＝0                          D.2m2＋m＝－1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：6cos60°-（sin21°-1）0×5tan45°;

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，点A在第一象限，⊙A与x轴交于B（2，0）、C（8，0）两点，与y轴相切于点D，则点A 的坐标是（  ）

    A．（3，5）    B．（4，5）     C．（5，3）   D．（5，4）

    查看答案和解析>>

    同步练习册答案