练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
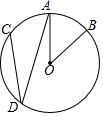
    17．如图，在⊙O中，$\widehat{AB}$=$\widehat{AC}$，∠AOB=40°，则∠ADC的度数是（　　）
    A．15°B．20°C．30°D．40°

    分析 先由圆心角、弧、弦的关系求出∠AOC=∠AOB=40°，再由圆周角定理即可得出结论．

    解答 解：连接CO，如图：
    ∵在⊙O中，$\widehat{AB}$=$\widehat{AC}$，
    ∴∠AOC=∠AOB，
    ∵∠AOB=40°，
    ∴∠AOC=40°，
    ∴∠ADC=$\frac{1}{2}$∠AOC=20°，
    故选B．

    点评 本题考查了圆心角、弧、弦的关系，圆周角定理；熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．先化简，再求值$\frac{{{x^2}-{y^2}}}{{{x^2}-2xy+{y^2}}}•\frac{x-y}{x+y}-\frac{x}{x-y}$，其中x=1+$\sqrt{2}，y=1-\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．△ABC中，∠C=60°，∠A、∠B的平分线交于O，则∠AOB=120°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知2+$\sqrt{3}$的小数部分为m，2-$\sqrt{3}$的小数部分为n，求（m+n）2015的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

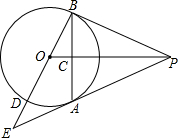    12．如图△PAB中，PA=PB，PB为⊙O的切线，B为切点，连接OP交AB于点C，延长BO与⊙O交于点D、与PA的延长线交于点E
    （1）求证：PA与⊙O相切；
    （2）若tan∠ABE=$\frac{1}{2}$，求sinE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

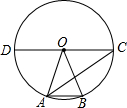    2．如图，在⊙O中，CD是直径，点A，点B在⊙O上，连接OA、OB、AC、AB，若∠AOB=40°，CD∥AB，则∠BAC的大小为（　　）
    A．30°B．35°C．40°D．70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，是某副食品公司销售糖果的总利润y（元）与销售量x（千克）之间的函数图象（总利润=总销售额-总成本），该公司想通过“不改变总成本，提高糖果售价”的方案解决销售不佳的现状，下面给出的四个图象，虚线均表示新的销售方案中总利润与销售量之间的函数图象，则能反映该公司改进方案的是（　　）
    A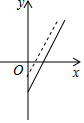．B．C．D．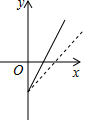

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在直角坐标系中，点P的坐标是（n，0）（n＞0），抛物线y=-x2+bx+c经过原点O和点P，已知正方形ABCD的三个顶点为A（2，2），B（3，2），D（2，3）．
    （1）若当n=4时求c，b并写出抛物线对称轴及y的最大值；
    （2）求证：抛物线的顶点在函数y=x2的图象上；
    （3）若抛物线与直线AD交于点N，求n为何值时，△NPO的面积为1；
    （4）若抛物线经过正方形区域ABCD（含边界），请直接写出n的取值范围．
    （参考公式：y=ax2+bx+c（a≠0）的顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为2．

    查看答案和解析>>

    同步练习册答案