
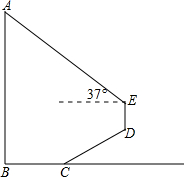
 cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$.计算结果保留根号)
cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$.计算结果保留根号) 分析 延长ED交BC延长线于点F,则∠CFD=90°,Rt△CDF中求得CF=CDcos∠DCF=2$\sqrt{3}$、DF=$\frac{1}{2}$CD=2,作EG⊥AB,可得GE=BF=4$\sqrt{3}$、GB=EF=3.5,再求出AG=GEtan∠AEG=4$\sqrt{3}$•tan37°可得答案.
解答 解:如图,延长ED交BC延长线于点F,则∠CFD=90°,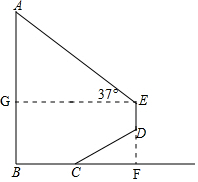
∵tan∠DCF=i=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠DCF=30°,
∵CD=4,
∴DF=$\frac{1}{2}$CD=2,CF=CDcos∠DCF=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴BF=BC+CF=2$\sqrt{3}$+2$\sqrt{3}$=4$\sqrt{3}$,
过点E作EG⊥AB于点G,
则GE=BF=4$\sqrt{3}$,GB=EF=ED+DF=1.5+2=3.5,
又∵∠AED=37°,
∴AG=GEtan∠AEG=4$\sqrt{3}$•tan37°,
则AB=AG+BG=4$\sqrt{3}$•tan37°+3.5=3$\sqrt{3}$+3.5,
故旗杆AB的高度为(3$\sqrt{3}$+3.5)米.
点评 本题主要考查解直角三角形的应用-仰角俯角问题和坡度坡比问题,掌握仰角俯角和坡度坡比的定义,并根据题意构建合适的直角三角形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
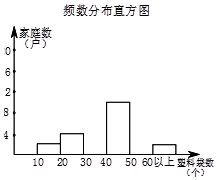 小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:| 组别 | 每月丢塑料袋个数 | 频数 | 频率 |
| 第1组 | 10至19 | 2 | 0.05 |
| 第2组 | 20至29 | 4 | 0.10 |
| 第3组 | 30至39 | 6 | 0.15 |
| 第4组 | 40至49 | 10 | 0.25 |
| 第5组 | 50至59 | 16 | 0.40 |
| 第6组 | 60以上 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.73)
如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com