
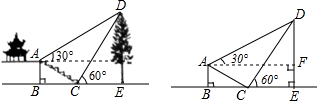
 阅读材料:
阅读材料:分析 (1)先根据路程=速度×时间求出A1A2=30$\sqrt{2}$×$\frac{1}{3}$=10$\sqrt{2}$,又A2B2=10$\sqrt{2}$,∠A1A2B2=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形;
(2)先由平行线的性质及方向角的定义求出∠A1B1B2=75°-15°=60°,由等边三角形的性质得出∠A2A1B2=60°,A1B2=A1A2=10$\sqrt{2}$,那么∠B1A1B2=105°-60°=45°.然后在△B1A1B2中,根据阅读材料可知,$\frac{{B}_{1}{B}_{2}}{sin45°}$=$\frac{{A}_{1}{B}_{2}}{sin60°}$,求出B1B2的距离,再由时间求出乙船航行的速度.
解答 解:(1)△A1A2B2是等边三角形,理由如下:
连结A1B2.
∵甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,航行20分钟到达A2,
∴A1A2=30$\sqrt{2}$×$\frac{1}{3}$=10$\sqrt{2}$,
又∵A2B2=10$\sqrt{2}$,∠A1A2B2=60°,
∴△A1A2B2是等边三角形;
(2)过点B作B1N∥A1A2,如图,
∵B1N∥A1A2,
∴∠A1B1N=180°-∠B1A1A2=180°-105°=75°,
∴∠A1B1B2=75°-15°=60°.
∵△A1A2B2是等边三角形,
∴∠A2A1B2=60°,A1B2=A1A2=10$\sqrt{2}$,
∴∠B1A1B2=105°-60°=45°.
在△B1A1B2中,
∵A1B2=10$\sqrt{2}$,∠B1A1B2=45°,∠A1B1B2=60°,
由阅读材料可知,$\frac{{B}_{1}{B}_{2}}{sin45°}$=$\frac{{A}_{1}{B}_{2}}{sin60°}$,
解得B1B2=$\frac{10\sqrt{2}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{20\sqrt{3}}{3}$,
所以乙船每小时航行:$\frac{20\sqrt{3}}{3}$÷$\frac{1}{3}$=20$\sqrt{3}$海里.
点评 本题考查了解直角三角形的应用-方向角问题,等边三角形的判定与性质,方向角的定义,锐角三角函数的定义,学生的阅读理解能力以及知识的迁移能力.正确理解阅读材料是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图△BCD中,BD=CD,作CD的垂直平分线AE,交BD的延长线于A,连结AC,已知△ACD的周长为30cm,△ABC的周长为48cm,则BC长为:18.
如图△BCD中,BD=CD,作CD的垂直平分线AE,交BD的延长线于A,连结AC,已知△ACD的周长为30cm,△ABC的周长为48cm,则BC长为:18.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
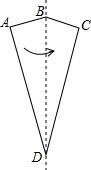 如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=2+$\sqrt{3}$或4+2$\sqrt{3}$.
如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=2+$\sqrt{3}$或4+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
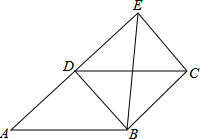 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )| A. | AB=BE | B. | BE⊥DC | C. | ∠ADB=90° | D. | CE⊥DE |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为2$\sqrt{3}$或2$\sqrt{7}$或2.
如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为2$\sqrt{3}$或2$\sqrt{7}$或2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
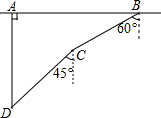 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com