
 如图,矩形纸片ABCD中,AB=3,BC=4;将纸片沿EF折叠,使B点与D点重合,则折痕EF的长是$\frac{15}{4}$.
如图,矩形纸片ABCD中,AB=3,BC=4;将纸片沿EF折叠,使B点与D点重合,则折痕EF的长是$\frac{15}{4}$. 分析 本题可利用相似解决,由于折叠,可知BD⊥EF,利用直角三角形相似的性质:对应边成比例求得结果.
解答 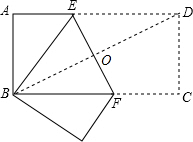 解:如图,连结BD交EF于O.
解:如图,连结BD交EF于O.
∵折叠纸片使点D与点B重合,
∴BD⊥EF,BO=DO
∵四边形ABCD是矩形,
∴∠C=90°,BD=$\sqrt{B{C}^{2}+A{B}^{2}}$=5,
∴BO=$\frac{5}{2}$,
∵BD⊥EF,
∴∠BOF=∠C=90°,
又∵∠CBD=∠OBF,
∴△BOF∽△BCD,
∴$\frac{BO}{BC}=\frac{OF}{CD}$,即$\frac{\frac{5}{2}}{4}$=$\frac{OF}{3}$,
∴OF=$\frac{15}{8}$,
∴EF=2OF=$\frac{15}{4}$.
故答案为:$\frac{15}{4}$.
点评 本题考查了翻折变换(折叠问题).折叠问题要要找清对应关系,重合的部分,重合的边,重合的角.这些关系在思考,做题时很有帮助.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P是抛物线y=x2-4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为(2+$\sqrt{2}$,1)或(2-$\sqrt{2}$,1)或(2,-1).
如图,P是抛物线y=x2-4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为(2+$\sqrt{2}$,1)或(2-$\sqrt{2}$,1)或(2,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com