
”¾ĢāÄæ”æijÉĢ³”¼Ę»®¾ĻśA”¢BĮ½ÖÖŠĀŠĶ½ŚÄÜĢØµĘ¹²50Õµ£¬ÕāĮ½ÖÖĢØµĘµÄ½ų¼Ū”¢ŹŪ¼ŪČēĻĀ±ķĖłŹ¾£®
AŠĶ | BŠĶ | |
½ų¼Ū£ØŌŖ/Õµ£© | 40 | 65 |
ŹŪ¼Ū£ØŌŖ/Õµ£© | 60 | 100 |
£Ø1£©ČōøĆÉĢ³”¹ŗ½ųÕāÅśĢØµĘ¹²ÓĆČ„2500ŌŖ£¬ĪŹÕāĮ½ÖÖĢصĘø÷¹ŗ½ų¶ąÉŁÕµ£æ
£Ø2£©ŌŚĆæÖÖĢصĘĻśŹŪĄūČó²»±äµÄĒéæöĻĀ£¬ČōøĆÉĢ³”ĻśŹŪÕāÅśĢØµĘµÄ×ÜĄūČó²»ÉŁÓŚ1400ŌŖ£¬ĪŹÖĮÉŁŠč¹ŗ½ųBÖÖĢØµĘ¶ąÉŁÕµ£æ
£Ø3£©ČōøĆÉĢ³”Ō¤¼ĘÓĆ²»ÉŁÓŚ2500ŌŖĒŅ²»¶ąÓŚ2600ŌŖµÄ׏½š¹ŗ½ųÕāÅśĢØµĘ£¬ĪŖĮĖ“ņæŖBÖÖĢØµĘµÄĻśĀ·£¬ÉĢ³”¾ö¶ØĆæŹŪ³öŅ»ÕµBÖÖĢØµĘ£¬·µ»¹¹ĖæĶĻÖ½šaŌŖ£Ø10£¼a£¼20£©£¬ĪŹøĆÉĢ³”øĆČēŗĪ½ų»õ£¬²ÅÄÜ»ńµĆ×ī“óµÄĄūČó£æ
”¾“š°ø”æ£Ø1£©øĆÉĢ³”¹ŗ½ųAÖÖĢصĘ30Õµ£¬¹ŗ½ųBÖÖĢصĘ20Õµ£»£Ø2£©ÖĮÉŁŠč¹ŗ½ųBÖÖĢصĘ27Õµ£»£Ø3£©¹ŗ½ųAÖÖĢصĘ26Õµ£¬¹ŗ½ųBÖÖĢصĘ24Õµ£¬øĆÉĢ³”»ńµĆµÄ×ÜĄūČó×ī“󣬹ŗ½ųAÖÖĢصĘ30Õµ£¬¹ŗ½ųBÖÖĢصĘ20Õµ£¬øĆÉĢ³”»ńµĆµÄ×ÜĄūČó×ī“ó£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Ź×ĻČÉčøĆÉĢ³”¹ŗ½ųAÖÖĢصĘxÕµ£¬¹ŗ½ųBÖÖĢØµĘ£Ø50©x£©Õµ£¬Č»ŗóøł¾ŻĢāŅā£¬¼“æɵƷ½³Ģ£¬½ā·½³Ģ¼“æÉĒóµĆ“š°ø£»
£Ø2£©ÉčÖĮÉŁŠč¹ŗ½ųBÖÖĢصĘxÕµ£¬Č»ŗóÓÉøĆÉĢ³”ĻśŹŪÕāÅśĢØµĘµÄ×ÜĄūČó²»ÉŁÓŚ1400ŌŖ£¬¼“æɵĆŅ»ŌŖŅ»“Ī²»µČŹ½35y+20£Ø50©y£©”Ż1400£¬½ā“Ė²»µČŹ½¼“æÉĒóµĆ“š°ø£»
£Ø3£©Ź×ĻČÉčøĆÉĢ³”¹ŗ½ųAÖÖĢصĘmÕµ£¬ÓÉøĆÉĢ³”Ō¤¼ĘÓĆ²»ÉŁÓŚ2500ŌŖĒŅ²»¶ąÓŚ2600ŌŖµÄ׏½š¹ŗ½ųÕāÅśĢØµĘ£¬æÉĶعż²»µČŹ½×éĒóµĆmµÄȔֵ·¶Ī§£¬Č»ŗóĒóµĆøĆÉĢ³”»ńµĆµÄ×ÜĄūČóÓėøĆÉĢ³”¹ŗ½ųAÖÖĢØµĘµÄÕµŹżµÄŅ»“ĪŗÆŹż£¬ÓÉ10£¼a£¼20£¬øł¾ŻŅ»“ĪŗÆŹżµÄŌö¼õŠŌ¼“æÉĒóµĆ“š°ø£®
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø1£©ÉčøĆÉĢ³”¹ŗ½ųAÖÖĢصĘxÕµ£¬¹ŗ½ųBÖÖĢØµĘ£Ø50©x£©Õµ£¬ÓÉĢāŅāµĆ£ŗ40x+65£Ø50©x£©=2500£¬½āµĆ£ŗx=30£¬”ąøĆÉĢ³”¹ŗ½ųAÖÖĢصĘ30Õµ£¬¹ŗ½ųBÖÖĢصĘ20Õµ£®
£Ø2£©Éč¹ŗ½ųBÖÖĢصĘyÕµ£¬ÓÉĢāŅāµĆ£ŗ35y+20£Ø50©y£©”Ż1400£¬½āµĆ£ŗy”Ż![]() £¬”ąyµÄ×īŠ”ÕūŹż½āĪŖ27£¬”ąÖĮÉŁŠč¹ŗ½ųBÖÖĢصĘ27Õµ£»
£¬”ąyµÄ×īŠ”ÕūŹż½āĪŖ27£¬”ąÖĮÉŁŠč¹ŗ½ųBÖÖĢصĘ27Õµ£»
£Ø3£©ÉčøĆÉĢ³”¹ŗ½ųAÖÖĢصĘmÕµ£¬ÓÉĢāŅāµĆ£ŗ2500”Ü40m+65£Ø50©m£©”Ü2600£¬½āµĆ£ŗ26”Üm”Ü30£¬ÉčøĆÉĢ³”»ńµĆµÄ×ÜĄūČóĪŖwŌŖ£¬Ōņw=20m+£Ø35©a£©£Ø50©m£©=£Øa©15£©m+1750©50a£®”ß10£¼a£¼20£¬”ąµ±10£¼a”Ü15Ź±£¬m=26£¬¼“¹ŗ½ųAÖÖĢصĘ26Õµ£¬¹ŗ½ųBÖÖĢصĘ24Õµ£¬øĆÉĢ³”»ńµĆµÄ×ÜĄūČó×ī“ó£»
µ±15£¼a£¼20Ź±£¬m=30£¬¼“¹ŗ½ųAÖÖĢصĘ30Õµ£¬¹ŗ½ųBÖÖĢصĘ20Õµ£¬øĆÉĢ³”»ńµĆµÄ×ÜĄūČó×ī“ó£®


 ĘŚÄ©ŗĆ³É¼ØĻµĮŠ“š°ø
ĘŚÄ©ŗĆ³É¼ØĻµĮŠ“š°ø 99¼Ó1ĮģĻČĘŚÄ©ĢŲѵ¾ķĻµĮŠ“š°ø
99¼Ó1ĮģĻČĘŚÄ©ĢŲѵ¾ķĻµĮŠ“š°ø °ŁĒæĆūŠ£ĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
°ŁĒæĆūŠ£ĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø ŗĆ³É¼Ø1¼Ó1ĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
ŗĆ³É¼Ø1¼Ó1ĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄ·½øńÖ½ÖŠ£¬Ć抔·½øńµÄ±ß³¤¶¼ĪŖ1.ĒėŌŚ·½øńÖ½ÉĻ»Ķ¼²¢»ŲČŻĪŹĢā£ŗŅŃÖŖµćA”¢B.
(1)»Ö±ĻßAB£¬ÉäĻßBC£»
(2)¹żµćC×÷“¹Ļ߶ĪCD”ĶAB£¬“¹×ćĪŖµćD.
(3)Į¬½įAC£¬Ōņ”÷ABCµÄĆ껿£½_______.
(4)ŅŃÖŖAB=5£¬ĒóĻ߶ĪCDµÄ³¤.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĆüĢāÖŠ¼ŁĆüĢāŹĒ£Ø £©
A.ŌŚĶ¬Ņ»Ę½ĆęÄŚ£¬ÓŠČżĢõÖ±Ļß![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬Čē¹ū
£¬Čē¹ū![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]()
B.µ±±»æŖ·½ŹżĄ©“óµ½100±¶Ź±£¬ĖćŹõĘ½·½øłµÄ½į¹ūĄ©“óµ½10±¶
C.ŌŚĶ¬Ņ»Ę½ĆęÄŚ£¬ÓŠČżĢõÖ±Ļß![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬Čē¹ū
£¬Čē¹ū![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]()
D.Ö±ĻßĶāŅ»µćµ½ÕāĢõÖ±Ļߵē¹Ļ߶ĪµÄ³¤¶Č£¬½Š×öµćµ½Ö±ĻߵľąĄė
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āijŠ£Ń§ÉśµÄÉķøßĒéæö£¬Ė껜³éČ”øĆŠ£ÄŠÉś”¢Å®Éś½ųŠŠ³éŃłµ÷²é£®
ŅŃÖŖ³éČ”µÄŃł±¾ÖŠ£¬ÄŠÉś”¢Å®ÉśµÄČĖŹżĻąĶ¬£¬ĄūÓĆĖłµĆŹż¾Ż»ęÖĘČēĻĀĶ³¼ĘĶ¼±ķ£ŗ£ØA×é£ŗx<155£»B×é£ŗ155”Üx<160£»C×é£ŗ160”Üx<165£»D×é165”Üx<170£»E×é£ŗx”Ż170£©
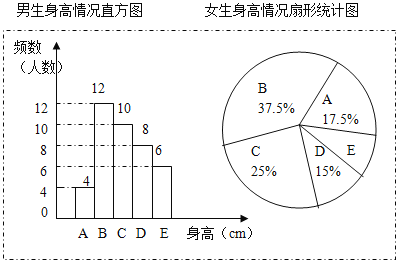
øł¾ŻĶ¼±ķĢį¹©µÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ńł±¾ÖŠ£¬ÄŠÉśµÄÉķøßÖŚŹżŌŚ ×飬֊Ī»ŹżŌŚ ×飮
£Ø2£©Ńł±¾ÖŠ£¬Å®ÉśµÄÉķøßŌŚE×éµÄČĖŹżÓŠ ČĖ£®
£Ø3£©ŅŃÖŖøĆŠ£¹²ÓŠÄŠÉś400ČĖ£¬Å®Éś380ČĖ£¬Ēė¹Ą¼ĘÉķøßŌŚ160”Üx<170Ö®¼äµÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬![]() µÄ¶„µć×ų±ź·Ö±šĪŖ
µÄ¶„µć×ų±ź·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬![]() .
.
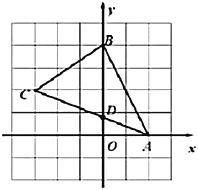
£Ø1£©Ēó![]() µÄĆ껿.
µÄĆ껿.
£Ø2£©Čō![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬ĒėĒó³ö
£¬ĒėĒó³ö![]() µćµÄ×ų±ź.
µćµÄ×ų±ź.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūA”¢B”¢CČżµćŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬ĒŅĻ߶ĪAB=6 cm£¬BC=4 cm£¬ČōM£¬N·Ö±šĪŖAB£¬BCµÄÖŠµć£¬ÄĒĆ“M£¬NĮ½µćÖ®¼äµÄ¾ąĄėĪŖ( )
A. 5 cm B. 1 cm C. 5»ņ1 cm D. ĪŽ·ØČ·¶Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµÆ»ÉŌ³¤(²»¹ŅÖŲĪļ)15cm£¬µÆ»É×ܳ¤L(cm)ÓėÖŲĪļÖŹĮæx(kg)µÄ¹ŲĻµČēĻĀ±ķĖłŹ¾£ŗ
µÆ»É×ܳ¤L(cm) | 16 | 17 | 18 | 19 | 20 |
ÖŲĪļÖŹĮæx(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
µ±ÖŲĪļÖŹĮæĪŖ4kg£ØŌŚµÆŠŌĻŽ¶ČÄŚ£©Ź±£¬µÆ»ÉµÄ×ܳ¤L(cm)ŹĒ_________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļß![]() ¹żµć
¹żµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() £ŗ
£ŗ![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() ½»ÓŚµćB£¬ÓėxÖį½»ÓŚµćC£®
½»ÓŚµćB£¬ÓėxÖį½»ÓŚµćC£®
£Ø1£©ĒókµÄÖµ£»
£Ø2£©ŗį”¢×Ż×ų±ź¶¼ŹĒÕūŹżµÄµć½Š×öÕūµć£®
¢Ł µ±b=4Ź±£¬Ö±½ÓŠ“³ö”÷OBCÄŚµÄÕūµćøöŹż£»
¢ŚČō”÷OBCÄŚµÄÕūµćøöŹżĒ”ÓŠ4øö£¬½įŗĻĶ¼Ļó£¬ĒóbµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
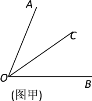
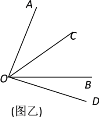
”¾ĢāÄæ”æŌĶĮĻĀĆę²ÄĮĻ£ŗŹżŃ§æĪÉĻ£¬ĄĻŹ¦øų³öĮĖČēĻĀĪŹĢā£ŗČēĶ¼¼×£¬”ĻAOB=70”ć£¬OCĘ½·Ö”ĻAOB£®
Čō”ĻBOD=20”ć£¬ĒėÄć²¹Č«Ķ¼ŠĪ£¬²¢Ēó”ĻCODµÄ¶ČŹż£®
ŅŌĻĀŹĒŠ”Ć÷µÄ½ā“š¹ż³Ģ£ŗ
½ā£ŗČēĶ¼ŅŅ£¬ŅņĪŖOCĘ½·Ö”ĻAOB£¬”ĻAOB=70”ć£¬
ĖłŅŌ”ĻBOC=____”ĻAOB=________”ć£®
ŅņĪŖ”ĻBOD=20”ć£¬
ĖłŅŌ”ĻCOD= ”ć£®
Š”¾²Ėµ£ŗ”°ĪŅ¾õµĆÕāøöĢāÓŠĮ½ÖÖĒéæö£¬Š”Ć÷æ¼ĀĒµÄŹĒODŌŚ”ĻAOBĶā²æµÄĒéæö£¬ŹĀŹµÉĻ£¬OD»¹æÉÄÜŌŚ”ĻAOBµÄÄŚ²æ”± £®
Ķź³ÉŅŌĻĀĪŹĢā£ŗ
£Ø1£©ĒėÄć½«Š”Ć÷µÄ½ā“š¹ż³Ģ²¹³äĶźÕū£»
£Ø2£©øł¾ŻŠ”¾²µÄĻė·Ø£¬ĒėÄćŌŚĶ¼¼×ÖŠ»³öĮķŅ»ÖÖĒéæö¶ŌÓ¦µÄĶ¼ŠĪ£¬Ēó³ö“ĖŹ±”ĻCODµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com