
 的图象分别与
的图象分别与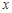 轴、
轴、 轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
 中,令
中,令 得:
得: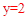 ;令
;令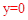 ,解得
,解得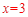 。
。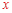 轴于点D。
轴于点D。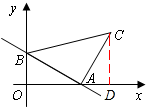
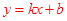 ,
,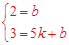 ,解得:
,解得: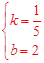 。
。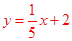 。
。

科目:初中数学 来源:不详 题型:解答题
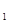 (元),节假日购票款为y
(元),节假日购票款为y (元)。y
(元)。y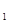 、y
、y 与x之间的函数图像如图所示
与x之间的函数图像如图所示
 , y
, y 与x之间的函数解析式
与x之间的函数解析式查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 成正比例,且
成正比例,且 时,
时,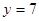 .
.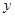 与
与 的函数关系式;
的函数关系式;  时,求
时,求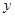 的值;
的值;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往 城,乙车驶往
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间 (时)之间的关系如图.
(时)之间的关系如图.
 关于
关于 的表达式;
的表达式; (千米).请直接写出
(千米).请直接写出 关于
关于 的表达式;
的表达式; (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com