
【题目】如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为____________ m.
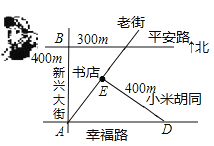
【答案】500
【解析】
由于BC∥AD,那么有∠DAE=∠ACB,由题意可知∠ABC=∠DEA=90°,BA=ED,利用AAS可证△ABC≌△DEA,于是AE=BC=300,再利用勾股定理可求AC,即可求CE,根据图可知从B到E的走法有两种,分别计算比较即可.
解:如图所示,设老街与平安路的交点为C.
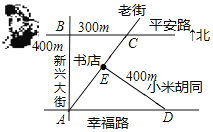
∵BC∥AD,
∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC=![]() =500m,
=500m,
∴CE=AC-AE=200m,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故答案是:500.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线m:y=x2﹣2x+2与直线l:y=x+2交于A,B(A在B的左侧),且抛物线顶点为C.
(1)求A,B,C坐标;
(2)若点D为该抛物线上的一个动点,且在直线AC下方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积.
(3)将抛物线m:y=x2﹣2x+2沿直线OC方向平移得抛物线m′,与直线l:y=x+2交于A′,B′,问在平移过程中线段A′B′的长度是否发生变化,请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
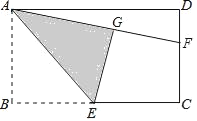
A.3![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②D是AC的中点;③AD=BD=BC;④△BDC的周长等于AB+BC.其中正确结论的个数有 .(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子里装有30个除颜色外其它均相同的球,其中红球有m个,白球有3m个,其它均为黄球.现小李从盒子里随机摸出一个球,若是红球,则小李获胜;小李把摸出的球放回盒子里摇匀,由小马随机摸出一个球,若为黄球,则小马获胜.
(1)当m=4时,求小李摸到红球的概率是多少?
(2)当m为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用![]() 万元购进这种衬衫,面市后果然供不应求.商厦又用
万元购进这种衬衫,面市后果然供不应求.商厦又用![]() 万元购进第二批这种衬衫,所购数量是第一批进量的
万元购进第二批这种衬衫,所购数量是第一批进量的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.商厦销售这种衬衫时每件定价
元.商厦销售这种衬衫时每件定价![]() 元,最后剩下
元,最后剩下![]() 件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com