练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，△ABC中，EF∥BC，PG∥AB，AP=CF，
    求证：△AEF≌△PGC．

    分析 根据全等三角形的判定证明即可．

    解答 证明：∵EF∥BC，PG∥AB，
    ∴∠C=∠AFE，∠GPC=∠A，
    又AP=CF，
    ∴AP+PF=CF+PF，
    ∴AF=PC，
    ∴由$\left\{\begin{array}{l}∠A=∠GPC\\∠AFE=∠C\\ AF=PC\end{array}\right.$，得△AEF≌△PGC．

    点评 本题考查了平行线的性质和全等三角形的应用，关键是推出证两三角形全等的三个条件，题目比较典型，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．如图，已知∠BDC=∠CEB=90°，BE、CD交于点O，且AO平分∠BAC，求证：OB=OC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，A2017的横坐标为（　　）
    A．1010B．2C．1D．-1006

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

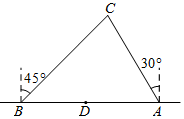    5．如图，两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻，同时发现一艘不明国籍船只停在C处海域，AB=60（$\sqrt{3}$+1）海里，在B处测得C在北偏东45°反向上，A处测得C在北偏西30°方向上，在海岸线AB上有一灯塔D，测得AD=100海里．
    （1）分别求出AC，BC（结果保留根号）．
    （2）已知在灯塔D周围80海里范围内有暗礁群，在A处海监穿沿AC前往C处盘查，途中有无触礁的危险？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，在平行四边形ABCD中，AE平分∠DAB，∠AED=26°，则∠C的度数为（　　）
    A．26°B．42°C．52°D．56°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．阅读理解：有一个n位自然数$\overline{{n_1}{n_2}{n_3}…{n_n}}$（n，n1，n2，n3，…nn是正整数，n≥2，1≤n1，n2，n3，…nn＜9），若交换不同数位上的数字得到一新数则叫这个n位自然数$\overline{{n_1}{n_2}{n_3}…{n_n}}$的一个“轮换数”，如：$\overline{{n_2}{n_1}{n_3}…{n_n}}$，$\overline{{n_1}{n_3}{n_2}…{n_n}}$均是$\overline{{n_1}{n_2}{n_3}…{n_n}}$的一个“轮换数”；36是63的一个“轮换数”，243是324的一个“轮换数”．
    （1）写出213的所有轮换数．
    （2）证明：任何一个3位自然数$\overline{{n_1}{n_2}{n_3}}$与它所有轮换数的和是111的倍数．
    （3）试求：4213与它所有轮换数的和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．一个不透明的袋子中，装有红黑两种颜色的小球（除颜色不同外其他都相同），其中一个红球，两个黑球．
    （1）小李从口袋中摸出一个球，摸出黑球的概率是多少？
    （2）小张第一次从口袋中摸出一个球，摸到红球不放回，摸到黑球放回；第二次又从口袋中摸出一个球，则小张第二次摸到黑球的概率是多少？试用树状图或列表法加以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，△ABO在直角坐标系中放置，A，B点坐标分别为（-2，4）和（-5，0），半径为2的⊙C与x轴相切于点B，与AB边交于点D．
    （1）如图1，若BE为⊙C的直径，连接AE，试说明AE是⊙O的切线；
    （2）如图2，若将⊙O向右平移，且⊙C始终与x轴相切，当切点为O时，点H为y轴右侧⊙C上一点，连接BH交⊙C于另一点G，问BG•BH是否为定值？若是，求出这个定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各运算中，计算正确的是（　　）
    A．a0=1B．$\sqrt{32}$-$\sqrt{8}$=2$\sqrt{2}$C．$\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$D．$\sqrt{18}$÷2=3

    查看答案和解析>>

    同步练习册答案