
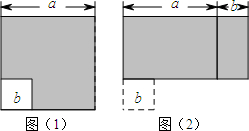
 如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.
如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.分析 (1)求出大正方形及小正方形的面积,作差即可得出阴影部分的面积,图(2)所示的长方形的长和宽分别为(a+b)、(a-b),由此可计算出面积;
(2)根据阴影部分的面积相等可得出平方差公式;
(3)利用原式补项(2-1),进而利用平方差公式求出答案.
解答 解:(1)∵大正方形的面积为a2,小正方形的面积为b2,
故图(1)阴影部分的面积值为:a2-b2,图(2)阴影部分的面积值为:(a+b)(a-b).
故答案为:a2-b2,(a+b)(a-b);
(2)以上结果可以验证乘法公式:a2-b2=(a+b)(a-b).
故答案为:a2-b2=(a+b)(a-b);
(3)原式=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1
=264-1+1
=264.
点评 本题考查了平方差公式的几何背景,注意几次分割后边的变化情况是关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
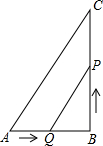 如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿 AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.
如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿 AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com