
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
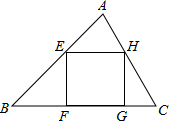 某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:
某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:鼎尖助学系列—同步练习(数学 八年级下册)、解直角三角形 勾股定理(1) 题型:022
在直角三角形中,三个内角度数的比为1∶2∶3,若斜边为a,则两条直角边的和为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com