
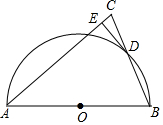
 如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E.
如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E.分析 (1)连接OD,AB为⊙0的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)连接AD.由AB为半圆O的直径,得到∠ADB=90°,根据垂直的定义得到∠DEC=∠ADB=90°.根据等腰三角形的性质得到CD=BD=$\frac{1}{2}$BC=3,根据相似三角形的性质即可得到结论.
解答 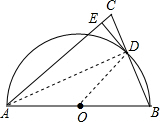 (1)证明:连接OD.
(1)证明:连接OD.
∵OD=OB,
∴∠ODB=∠OBD.
∵AB=AC,
∴∠ACB=∠OBD.
∴∠ACB=∠ODB.
∴OD∥AC,
∴∠DEC=∠ODE.
∵DE⊥AC,
∴∠DEC=90°.
∴∠ODE=90°,即OD⊥DE,
∵DE过半径OD的外端点D,
∴DE是⊙O的切线;
(2)解:连接AD.
∵AB为半圆O的直径,
∴∠ADB=90°,
∵DE⊥AC,
∴∠DEC=∠ADB=90°.
∵AB=AC,BC=6,
∴CD=BD=$\frac{1}{2}$BC=3,
又∵∠ECD=∠DBA,
∴△CED∽△BDA,
∴$\frac{CE}{BD}$=$\frac{CD}{BA}$.
∵CE=1,
∴$\frac{1}{3}$=$\frac{3}{BA}$.
∴AB=9,
∴半圆O的半径的长为4.5.
点评 本题考查了切线的判定定理:过半径的外端点且与半径垂直的直线为圆的切线.也考查了等腰三角形的性质、三角形相似的判定和性质.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:判断题
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数
(3)从样本数据为C级的人中随机抽取2人,用树状图或列表法求抽得2个人的“日均发微博条数”都是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com