
【题目】如图,直线y=![]() x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=
x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=![]() x+3上,若N点在第二象限内,则tan∠AON的值为( )
x+3上,若N点在第二象限内,则tan∠AON的值为( )
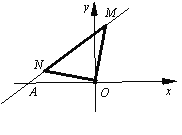
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
解:
过O作OC⊥AB于C,过N作ND⊥OA于D,

∵N在直线y="3" 4 x+3上,
∴设N的坐标是(x,3 4 x+3),
则DN=-(3 4 x+3),OD=-x,
y="3" 4 x+3,
当x=0时,y=3,
当y=0时,x=-4,
∴A(-4,0),B(0,3),
即OA=4,OB=3,
在△AOB中,由勾股定理得:AB=5,
∵在△AOB中,由三角形的面积公式得:AO×OB=AB×OC,
∴3×4=5OC,
OC="12" 5 ,
∵在Rt△NOM中,OM=ON,∠MON=90°,
∴∠MNO=45°,
∴sin45°="OC" ON ="12" 5 ON ,
∴ON="12" 2 5 ,
在Rt△NDO中,由勾股定理得:ND2+DO2=ON2,
即(-3 4 x-3)2+(-x)2="(12" 2 5 )2,
解得:x1="-84" 25 ,x2="12" 25 ,
∵N在第二象限,
∴x只能是-84 25 ,
3 4 x+3="12" 25 ,
即ND="12" 25 ,OD="84" 25 ,
tan∠AON="ND" OD ="1" 7 .
故选A.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AD是BC边上的高.∠BAF=∠CAG=90°,且AB=AF=AC=AG.连接FG,交DA的延长线于点E,连接BG,CF.下列结论:①∠FAG+∠BAC=180°;②BG=CF;③BG⊥CF;④∠EAF=∠ABC.其中一定正确的个数是( )
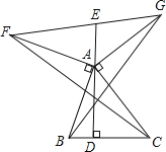
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
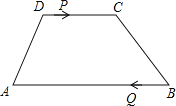
查看答案和解析>>
科目:初中数学 来源: 题型:
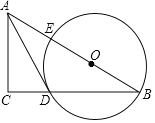
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
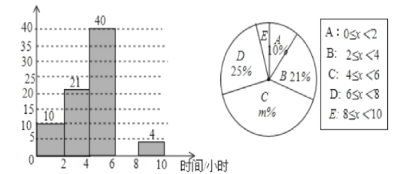
根据图中提供的信息,解答下列问题:
(1)共随机调查了___名学生,课外阅读时间在68小时之间有___人,并补全频数分布直方图;
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)请估计该校3000名学生每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.
(1)若将这种水果每千克的售价降低![]() 元,则每天销售量是多少千克?(结果用含
元,则每天销售量是多少千克?(结果用含![]() 的代数式表示)
的代数式表示)
(2)若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器上销售一种微波炉和电磁炉,微波炉每台定价![]() 元,电磁炉每台定价
元,电磁炉每台定价![]() 元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;
元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的![]() 付款;
付款;
现某客户要到该卖场购买微波炉![]() 台,电磁炉
台,电磁炉![]() 台
台![]()
(1)若该客户按方案一、方案二购买,分别需付款多少元?(用含![]() 的式子表示)
的式子表示)
(2)若![]() ,通过计算说明此时那种方案购买较为核算?
,通过计算说明此时那种方案购买较为核算?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
科目:初中数学 来源: 题型:
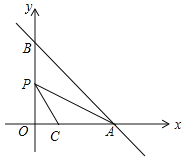
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 ;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com