
����Ŀ��ij��������Ʊ���۷����ࣺһ��Ϊɢ����Ʊ���۸�Ϊ![]() Ԫ/�ţ���һ��Ϊ������Ʊ��һ���Թ�����Ʊ
Ԫ/�ţ���һ��Ϊ������Ʊ��һ���Թ�����Ʊ![]() �����ϣ���ÿ����Ʊ�۸���ɢ����Ʊ�۸�Ļ����ϴ�
�����ϣ���ÿ����Ʊ�۸���ɢ����Ʊ�۸�Ļ����ϴ�![]() �ۣ�ij�ಿ��ͬѧҪȥ�þ������Σ���μ�����
�ۣ�ij�ಿ��ͬѧҪȥ�þ������Σ���μ�����![]() �ˣ�������Ʊ��Ҫ
�ˣ�������Ʊ��Ҫ![]() Ԫ
Ԫ
��1�����ÿ�˷ֱ���Ʊ����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�������������Ʊ����![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3������������仯���һ�ֱȽ�ʡǮ�Ĺ�Ʊ��ʽ.
���𰸡���1��![]() ����2��y=32x(x10)����3��8��������ɢ��Ʊ�� 8������������Ʊ��ǡ��8��ʱ�����ɰ�10��������Ʊ������ɢ��Ʊ.
����2��y=32x(x10)����3��8��������ɢ��Ʊ�� 8������������Ʊ��ǡ��8��ʱ�����ɰ�10��������Ʊ������ɢ��Ʊ.
��������
��1����ɢ����Ʊ�۸�Ϊ40Ԫ/�ţ�����Ʊ�۳��������ɣ���y=40x��
��2��������Ʊ����Ҫһ�ι�����Ʊ10�ż����ϣ���x��10�����ô��ۺ��Ʊ�۳��������ɣ�
��3�����ݣ�1����2�������̽�ֵó��𰸼��ɣ�
(1)ɢ����Ʊ��y=40x��
(2)����Ʊ��y=40��0.8x=32x(x10)��
(3)��Ϊ40��8=32��10��
���Ե�����Ϊ8�ˣ�x=8ʱ�����ֹ�Ʊ������ͬ��
����������8�ˣ�x<8ʱ����ɢ����Ʊ��Ʊ�Ƚ�ʡǮ��
����������8�ˣ�x>8ʱ��������Ʊ��Ʊ�Ƚ�ʡǮ.


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�͡�DCE�У�CA=CB��CD=CE����CAB= ��CED=��.
(1)��ͼ1����AD��EB�ӳ����ӳ����ཻ�ڵ�0.
����֤:BE= AD;
���ú�����ʽ�ӱ�ʾ��AOB�Ķ���(ֱ��д�����);
(2)��ͼ2,����=45��ʱ������BD��AE,��CM��AE��M�㣬�ӳ�MC��BD���ڵ�N.��֤:N��BD���е�.
ע:��(2)�ʵĽ���������ע������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л��Ļ�ʮ���ԴԶ�������ҹ��Ŵ���ѧ��������ɾ�㷨ͳ�ڡ����ء��������͡����⣺��һ������һ���������ȸ��Ӷ�һ�С�������� Ϊ������һ���ͺ�һҪ�������ۻ����������ͣ�ȴ�ȸͳߣ�������������ۺ���ȥ���ͺ�һ��������������ȥ���ͣ������ȸͳ�5�ߣ�����������ۺ���ȥ���ͣ��ͱȸͶ�5��.��������![]() �ߣ��ͳ�
�ߣ��ͳ�![]() �ߣ����������ķ������ǣ� ��
�ߣ����������ķ������ǣ� ��
A. 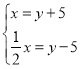 B.
B. 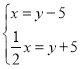 C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�DE��AB��BF��CD������ֱ�ΪE��F��
��1����֤����ADE�ա�CBF��
��2����֤���ı���BFDEΪ���Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ�������ֱ�ΪA(1,-2)��B(4,-1)��C(3,-3).
��1����������ABC����ƽ��5����λ��������ƽ��3����λ��ġ�A1B1C1����д����B�Ķ�Ӧ��B1������____________��
��2����ԭ��OΪλ�����ģ���λ�����ĵ�ͬ�����A1B1C1��һ��λ�ơ�A2B2C2��ʹ�����A1B1C1�����Ʊ�Ϊ2:1����д����B1�Ķ�Ӧ��B2������____________��
��3������A1B1C1�ڲ�����һ��P1 ������Ϊ(a-5,b+3)��ֱ��д��������2���ı仯���P1�Ķ�Ӧ��P2�����꣨�ú�a��b�Ĵ���ʽ��ʾ����P2��������____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x���ཻ��A����3��0����B��1��0�����㣬��y���ཻ�ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��

��1����D�����ꣻ
��2������κ����Ľ���ʽ��
��3������ͼ��ֱ��д��ʹһ�κ���ֵС�ڶ��κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��F��BD�ϣ�BE=DF��
��1����֤��AE=CF��
��2����AB=6����COD=60���������ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD��EF�ཻ�ڵ�O����AOE����AOD=1��3����COB����DOF=3��4�����DOE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ����һ�κ���y=kx+4m��m��0����ͼ����B��p��2m��������m��0��
��1����m=1����k=��1�����B��������
��2����֪��A��m��0������ֱ��y=kx+4m��x�ύ�ڵ�C��n��0����n+2p=4m�����ж��߶�AB���Ƿ����һ��N��ʹ�õ�N������ԭ��O�뵽��C�ľ���֮�͵����߶�OB�ij�����˵��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com