
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
.
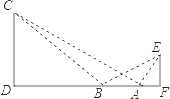
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
【答案】(1)旗杆EF的高为5![]() 米;(2)旗杆EF与实验楼CD之间的水平距离DF的长是45米
米;(2)旗杆EF与实验楼CD之间的水平距离DF的长是45米
【解析】
(1)根据题目中的数据和锐角三角函数可以求得EF和AF的长,从而可以解答本题;
(2)根据题目中的数据和锐角三角函数可以求得AD和AF的长,从而可以得到旗杆EF与实验楼CD之间的水平距离DF的长.
(1)解:∵∠EAF=60°,然后向左移动10米到B处,
测得∠EBF=30°,∠CBD=45°,tan∠CAD=![]() ,
,
∴tan60°=![]() ,tan30°=
,tan30°=![]() ,
,
解得,EF=![]() ,AF=5,
,AF=5,
即旗杆EF的高为![]() 米;
米;
(2)解:∵∠EAF=60°,然后向左移动10米到B处,
测得∠EBF=30°,∠CBD=45°,tan∠CAD=![]() ,AF=5,
,AF=5,
∴CD=BD,![]() ,
,
设CD=3a,则BD=3a,AD=4a,
∴AB=a=10,
∴BD=3a=30,
∴DF=AD+AF=40+5=45,
即旗杆EF与实验楼CD之间的水平距离DF的长是45米.


科目:初中数学 来源: 题型:
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
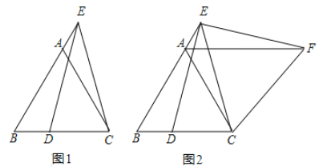
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一抛物线的顶点坐标是
中,一抛物线的顶点坐标是![]() ,且过点
,且过点![]() ,平行四边形
,平行四边形![]() 的顶点在
的顶点在![]() 此抛物线上,
此抛物线上,![]() 与
与![]() 轴相交于点
轴相交于点![]() .己知点
.己知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是抛物线上任意一点.
是抛物线上任意一点.
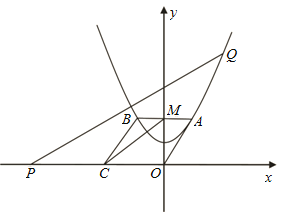
(1)求此抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在抛物线上是否存在点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍?若存在,求此时点
的面积的2倍?若存在,求此时点![]() 的坐标.
的坐标.
(3)在![]() 轴上有一动点
轴上有一动点![]() ,若
,若![]() ,试建立
,试建立![]() 关于
关于![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的运动范围;
的运动范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.
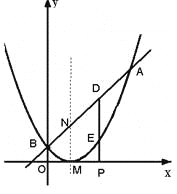
(1)求m的值及这个二次函数的解析式;
(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织“优质课大赛”活动,经过评比有两名男教师和两名女教师获得一等奖,学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛,挑选的两位教师恰好是一男一女的概率为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
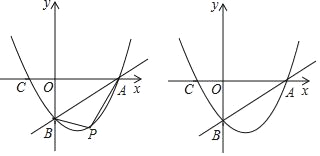
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“疾驰臭豆腐”是长沙知名地方小吃,某分店经理发现,当每份臭豆腐的售价为![]() 元时,每天能卖出
元时,每天能卖出![]() 份;当每份臭豆腐的售价每增加
份;当每份臭豆腐的售价每增加![]() 元时,每天就会少卖出
元时,每天就会少卖出![]() 份,设每份臭豆腐的售价增加
份,设每份臭豆腐的售价增加![]() 元时,一天的营业额为
元时,一天的营业额为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出
的函数关系式(不要求写出![]() 的取值范围);
的取值范围);
(2)考虑到顾客可接受价格![]() 元
元![]() 份的范围是
份的范围是![]() ,且
,且![]() 为整数,不考虑其他因素,则该分店的臭豆腐每份多少元时,每天的臭豆腐营业额最大?最大营业额是多少元?
为整数,不考虑其他因素,则该分店的臭豆腐每份多少元时,每天的臭豆腐营业额最大?最大营业额是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com