练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知点都在二次函数的图象上，则y1, y2 , y3的大小关系是______ 。

    【解析】试题分析：把A（4，y1），B（，y2），C（－2，y3）分别代入y＝(x－2)2－1得： y1＝(4－2)2－1＝3，y2＝(－2)2－1＝5－，y3＝(－2－2)2－1＝15， ∵5－＜3＜15， 所以y3＞y1＞y2． 故答案为：y3＞y1＞y2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：填空题

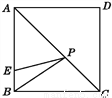
    如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是__________. 

    10 【解析】试题分析：根据题意得：AE=6，AD=AB=8，根据正方形的性质可得点B关于AC的对称轴为点D，连接DE，DE与AC的交点就是点P，则DE==10．

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：解答题

    计算： +（﹣1）0﹣|﹣3|．

    1 【解析】试题分析：任何非零实数的零次幂为1，负数的绝对值等于它的相反数，9的算术平方根为3，然后进行有理数的加减法计算． 试题解析：【解析】 原式=3+1﹣3=1．

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：单选题

    实数的值在（　　）

    A. 0和1之间 B. 1和2之间 C. 2和3之间 D. 3和4之间

    D 【解析】试题分析：因为，则，故处在3和4之间，故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：解答题

    如图,已知A(?4,2)、B(a,?4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点；

    (1)求此反比例函数和一次函数的解析式；

    (2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围；

    (1)反比例函数的解析式为，一次函数的解析式为y=-x-2（2）-42 【解析】试题分析：（1）把A点坐标代入反比例函数解析式求出m的值，再把B点坐标代入反比例函数解析式求出a的值，从而得出点B的坐标，根据点A、B的坐标利用待定系数法即可求出直线AB的解析式； （2）由两函数图象的上下位置关系结合交点的横坐标，即可得出使一次函数值小于反比例函数值的x的取值范围． 试...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    已知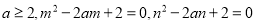，则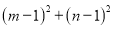的最小值是（  ）。

    A. 6 B. 3 C. -3 D. 0

    A 【解析】试题分析：∵m2－2am＋2＝0，n2－2an＋2＝0， ∴m，n是关于x的一元二次方程x2－2ax＋2＝0的两个根， ∴m＋n＝2a，mn＝2， ∴(m－1)2＋(n－1)2＝m2－2m＋1＋n2－2n＋1＝(m＋n)2－2mn－2(m＋n)＋2＝4a2－4－4a＋2＝4(a－)2－3， ∵a≥2， ∴当a＝2时，(m－1)2＋(n－1)2有最小值...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    如图,已知的半径为10,弦,M是AB上任意一点,则线段OM的长可能是(    )

    A. 5 B. 7 C. 9 D. 11

    C 【解析】试题分析：过点O作OM′⊥AB，垂足为M，连接OA， ∵OM⊥AB，AB＝12 ∴AM′＝BM′＝6， 在Rt△OAM中，OM′＝＝8， ,所以8≤OM≤10， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：单选题

    对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b；如：max{4，﹣2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，﹣x+1}，则该函数的最小值是（　　）

    A. 0 B. 2 C. 3 D. 4

    B 【解析】试题分析：当x+3≥﹣x+1，即：x≥﹣1时，y=x+3，∴当x=﹣1时，ymin=2， 当x+3＜﹣x+1，即：x＜﹣1时，y=﹣x+1，∵x＜﹣1，∴﹣x＞1，∴﹣x+1＞2，∴y＞2，∴ymin=2，

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，在△ABC中，点P、Q分别是BC、AC边上的点，PSAC，PRAB，若AQPQ，PR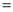PS，则下列结论：①ASAR；②QP∥AR；③△BRP ≌△CPS；④S四边形ARPQ=．其中正确的结论有____________（填序号）.

    ①② 【解析】连接AP. ∵PR=PS，AP=AP，PR⊥AB，PS⊥AC， ∴△APR≌△APS， ∴AS=AR，①正确. ∵PR=PS，PR⊥AB，PS⊥AC， ∴AP是∠BAC的平分线， ∴∠BAP=∠QAP. ∵AQ=PQ， ∴∠QAP=∠QPA， ∴∠BAP=∠QPA， ∴QP∥AR，②正确. 点P是BC的上的点，并...

    查看答案和解析>>

    同步练习册答案