
问题提出
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一
直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
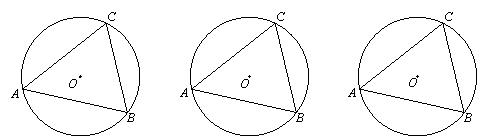
⑴当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);

由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
 |
此时有 , 此时有 , 此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
 (3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
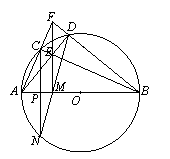
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA, CB;
CB;
②在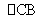 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
(1)同弧所对的圆周角相等.
∠ACB<∠ADB,∠ACB>∠ADB.
答案不惟一,如:∠ACB=∠ADB.
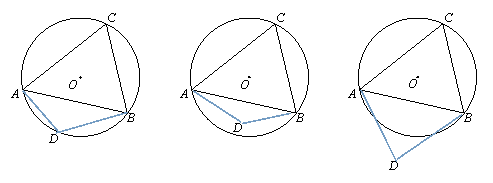 (2)如图:
(2)如图:
此时∠ACB+∠ADB=180°, 此时∠ACB+∠ADB>180°, 此时∠ACB+∠ADB<180
若四点组成的四边形对角互补,则这四点在同一个圆上.
(3)作图正确.
 ∵AB是⊙O的直径,C、D在⊙O上,
∵AB是⊙O的直径,C、D在⊙O上,
∴∠ACB=90°,∠ADB=90°.
∴点E是△ABF三条高的交点.
∴FM⊥AB.
∴∠EMB=90°.
∠EMB+∠EDB=180°,
∴点E,M,B,D在同一个圆上.
∴∠EMD=∠DBE.
又∵点N,C,B,D在⊙O上,
∴∠DBE=∠CND,∠EMD=∠CND.
∴FM∥CN.
∴∠CPB=∠EMB=90°.
∴CN⊥AB.
(注:其他正确的说理方法参照给分.)


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
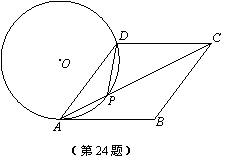
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC=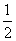 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
某科研机构对我区400户有两个孩子的家庭进行了调查,得到了
表格中的数据,其中(男,女)代表第一个孩子是男孩,第二个孩子
是女孩,其余类推.由数据,请估计我区两个孩子家庭中男孩与女
孩的人数比为 : .
| 类别 | 数量(户) |
| (男,男) | 101 |
| (男,女) | 99 |
| (女,男) | 116 |
| (女,女) | 84 |
| 合计 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解南京市2012年市城镇非私营单位员工每月的收入状况,统计局对市城镇
非私营单位随机抽取了1000人进行抽样调查.整理样本数据,得到下列图表:
市城镇非私营单位1000人月收入频数分布表
| 月工资x(元) | 频数(人) |
| x<2000 | 60 |
| 2000≤x<4000 | 610 |
| 4000≤x<6000 | 180 |
| 6000≤x<8000 | 50 |
| x≥8000 | 100 |
| 合计 | 1000 |
(1)如果1000人全部在金融行业抽取,这样的抽样是否合理?请说明理由;
(2)根据这样的调查结果,绘制条形统计图;
(3)2012年南京市城镇非私营单位月平均工资为5034元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com