【题目】如图，正九边形
中，
，那么
的长是________．
【答案】
【解析】
先由多边形的内角和定理，求出正九边形内角的度数，由圆周角定理可求出∠CAB＝20°，连接AH，作HM，GN分别垂直AE于M，N，再求出△AHM中各角的度数，由正方形的性质及直角三角形的性质即可解答．
∵正九边形内角和为（92）×180°＝1260°，
∴每个内角为140°，
又∵AB＝AC，∠B＝140°，
∴∠CAB＝（180°140°）÷2＝20°，
连接AH，作HM，GN分别垂直AE于M，N，
∵∠CAE＝2∠CAB＝2×20°＝40°．
∴∠HAM＝140°2×20°40°＝60°，
∴∠AHM＝30°，
设AM＝EN＝x，MN＝y，
四边形HGNM是矩形，所以HG＝y，即正九边形边长为y，
在Rt△AHM中，∠AHM＝∠30°，
∴AH＝2AM＝2x，
∴AB＋AC＝y＋2x，
而x＋y＋x＝1，
∴2x＋y＝1，
∴AB＋AC＝1．
故答案为：1．
科目：初中数学 来源： 题型：
【题目】如图
、
是两条垂直的公路，设计时想在拐弯处用一段圆弧形弯道把它们连接起来（圆弧在
、
两处分别与道路相切），测得
米，
．
在图中画出圆弧形弯道的示意图（用尺规作图，保留作图痕迹，不写作法与证明）；
计算弯道部分的长度（结果用
表示并保留根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝（m+1）x+
的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB的面积为
．
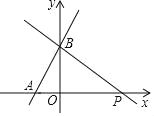
（1）求m的值及点A的坐标；
（2）过点B作直线BP与x轴的正半轴相交于点P，且OP＝3OA，求直线BP的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
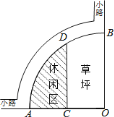
【题目】小明家住房结构如图所示（x、y的单位：米）．
（1）请用含x、y的代数式表示该住房的面积；
（2）小明爸爸打算把卧室铺上木地板，其余地面都铺上地砖，至少要买多少平方米的木地板材料？（用含x、y的代数式表示）如果每平方米地砖的价格是a元，则购买地砖至少需要多少钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你利用上述方法求出△ABC的面积．
（2）在图2中画△DEF，DE、EF、DF三边的长分别为
、
、
①判断三角形的形状，说明理由．
②求这个三角形的面积．（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示是某公园为迎接“中国–南亚博览会”设置的一休闲区．
，弧
的半径
长是
米，
是的中点，点
在弧上，
，则图中休闲区（阴影部分）的面积是（ ）
A. 
米2 B. 
米2 C. 
米2 D. 
米2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，在BC边上有两动点D、E，满足2∠DAE=∠BAC，将△AEC绕A旋转，使得AC与AB重合，点E落到点E’．
（1）求证：∠DAE’=∠DAE；
（2）当∠BE’D=20°时，求∠DEA的度数；
（3）当BD=1，EC=2，△BE’D又为直角三角形时，求∠BAC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
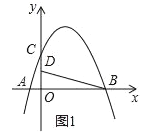
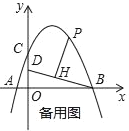
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+4交x轴于点A（﹣2，0）和B（B在A右侧），交y轴于点C，直线y=
经过点B，交y轴于点D，且D为OC中点．
（1）求抛物线的解析式；
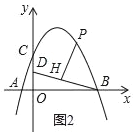
（2）若P是第一象限抛物线上的一点，过P点作PH⊥BD于H，设P点的横坐标是t，线段PH的长度是d，求d与t的函数关系式；
（3）在（2）的条件下，当d=
时，将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠ABC＝90°，AB＝
BC，∠ABC的平分线BD交过点C且平行AB的直线于D点；AE⊥BD交BD于E点，连接CE并延长，交过A点且平行BC的直线于F点，AD与CF交于O点．现得到如下两个结论：①∠DAE＝22.5°；②DE＝（2-）BE；
请帮助判断结论的真假，并说明你的理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com