
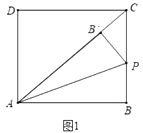
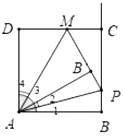
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.


(1)当![]() 时.
时.
①如图2.当点![]() 落在
落在![]() 上时,显然
上时,显然![]() 是直角三角形,求此时
是直角三角形,求此时![]() 的值;
的值;
②当点![]() 不落在
不落在![]() 上时,请直接写出
上时,请直接写出![]() 是直角三角形时
是直角三角形时![]() 的值;
的值;
(2)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且当
,且当![]() 时,
时,![]() .问:当
.问:当![]() ,
,![]() 的大小是否发生变化,若不变,请说明理由.
的大小是否发生变化,若不变,请说明理由.
【答案】(1)①![]() ,②
,②![]() 或
或![]() 或
或![]() ;(2)不变,见解析
;(2)不变,见解析
【解析】
(1)①利用勾股定理求出AC,再根据折叠的性质以及勾股定理即可得出答案;②分三种情况进行讨论:①如图2-1中,当![]() 时,②如图2-2中,当
时,②如图2-2中,当![]() 时,③如图2-3中,当
时,③如图2-3中,当![]() 时,在
时,在![]() 中分别找出每条边的长度,再利用勾股定理建立方程求解即可得出答案;
中分别找出每条边的长度,再利用勾股定理建立方程求解即可得出答案;
(2)首先证明ABCD是正方形,再利用全等三角形的性质以及折叠的性质即可得出答案.
解:(1)①如图1中,∵四边形![]() 是矩形,
是矩形,
∴![]() ,∴
,∴![]()
∵翻折
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴在![]() 中,
中,![]()
∴![]()
∴![]() ;
;
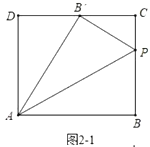
②如图2-1中,当![]() ,
,![]() 在
在![]() 上时,
上时,
∵四边形![]() 是矩形,∴
是矩形,∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]()
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() .
.
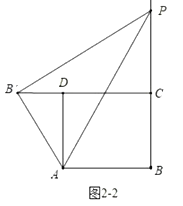
如图2-2中,当![]() ,
,![]() 在
在![]() 的延长线上时,
的延长线上时,
在![]() 中,
中,![]() ,
,
∴![]()
在![]() 中,则有:
中,则有:![]() ,
,
解得![]() .
.
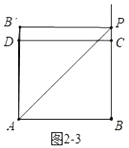
如图2-3中,当![]() 时,
时,
易证四边形![]() 为正方形,则
为正方形,则![]() .
.
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() ;
;
(2)当![]() 时,如图,∵
时,如图,∵![]()
∴![]() ,
,![]()
∵翻折,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即四边形
,即四边形![]() 是正方形,
是正方形,
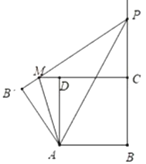
当![]() 时,如图,设
时,如图,设![]()
∴![]() ,
,
∴![]() ,
,
易证![]() ,
,
∴![]() ,
,
∵翻折,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】作图,思考并回答问题:如图,已知:ABC
(1)按下列要求作图:取边AB、AC的中点D、E,连结线段DE;
(2)用刻度尺测量线段 DE、BC的长度分别为 ;
(3)用量角器得![]() B与
B与![]() ADE的度数分别为 ;
ADE的度数分别为 ;
(4)通过(2)、(3)你发现DE与BC什么关系?请写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖的长方体盒子,如果这个无盖的长方体底面积为160cm2,那么该长方体盒子体积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,正方形![]() 的两边分别在正方形
的两边分别在正方形![]() 的边
的边![]() 和
和![]() 上,连接
上,连接![]() .填空:线段
.填空:线段![]() 与
与![]() 的数量关系为________;直线
的数量关系为________;直线![]() 与
与![]() 所夹锐角的大小为________.
所夹锐角的大小为________.



(2)如图②,将正方形![]() 绕点
绕点![]() 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
(3)把图②中的正方形都换成菱形,且![]() ,如图③,直接写出
,如图③,直接写出![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:

(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:在学习绝对值时,老师教过我们绝对值的几何含义,![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 在数轴上对应的点到原点的距离,一般地,点
在数轴上对应的点到原点的距离,一般地,点![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() ,那么
,那么![]() 、
、![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
(![]() )点
)点![]() 、
、![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到
到![]() 的距离表示为______________________________(用含绝对值的式子表示).如果
的距离表示为______________________________(用含绝对值的式子表示).如果![]() ,那么
,那么![]() 为______________________________.
为______________________________.
(![]() )利用数轴探究:
)利用数轴探究:
①找出满足![]() 的
的![]() 的所有整数值是____________________;
的所有整数值是____________________;
②设![]() ,当
,当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,
的范围时,![]() 的值是不变的,而且是
的值是不变的,而且是![]() 的最小值,这个最小值是____________________;
的最小值,这个最小值是____________________;
(![]() )求
)求![]() 的最小值为____________________,此时
的最小值为____________________,此时![]() 的值为____________________.
的值为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com