
分析 (1)根据题意k≠0,△>0,列出不等式组即可解决问题.
(2)设反比例函数解析式为y=$\frac{m}{x}$,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.
(3)结论:$\frac{{Q}_{1}P•{Q}_{2}P}{{Q}_{1}{Q}_{2}}$=1.令y=0,则有kx2+$\frac{1}{2}$x+$\frac{15}{4}$=0,所以xA+xB=-$\frac{1}{2k}$,xA•xB=$\frac{15}{4k}$,根据xA2+xB2=34,列出方程求出k的值,设过点P的直线为y=kx+3-k,
由由$\left\{\begin{array}{l}{y=kx+3-k}\\{y=-\frac{1}{4}{x}^{2}+\frac{1}{2}x+\frac{15}{4}}\end{array}\right.$消去y得x2+(4k-2)x-3-4k=0,得x1+x2=-(4k-2),x1x2=-3-4k,根据$\frac{{Q}_{1}P•{Q}_{2}P}{{Q}_{1}{Q}_{2}}$=$\frac{\sqrt{({x}_{1}-1)^{2}+({y}_{1}-3)^{2}}•\sqrt{({x}_{2}-1)^{2}+({y}_{2}-3)^{2}}}{\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}}$,代入化简即可解决问题.
解答 解:(1)∵二次函数y=kx2+$\frac{1}{2}$x+$\frac{15}{4}$与x轴有两个不同的交点,
∴$\left\{\begin{array}{l}{k≠0}\\{\frac{1}{4}-4k•\frac{15}{4}>0}\end{array}\right.$,
解得k<$\frac{1}{60}$且k≠0.
(2)设反比例函数解析式为y=$\frac{m}{x}$,
∵经过点(1,k),
∴m=k,
∵反比例函数和二次函数y=kx2+$\frac{1}{2}$x+$\frac{15}{4}$都是y随x的增大而增大,
∴k<0,
x<-$\frac{\frac{1}{2}}{2k}$,即x<-$\frac{1}{4k}$.
(3)结论:$\frac{{Q}_{1}P•{Q}_{2}P}{{Q}_{1}{Q}_{2}}$=1.
理由:令y=0,则有kx2+$\frac{1}{2}$x+$\frac{15}{4}$=0,
∴xA+xB=-$\frac{1}{2k}$,xA•xB=$\frac{15}{4k}$,
∵xA2+xB2=34,
∴(xA+xB)2-2xA•xB=34,
∴($\frac{1}{2k}$)2-$\frac{15}{2k}$-34=0,
解得k=-$\frac{1}{4}$或$\frac{1}{34}$
由(1)可知k<$\frac{1}{60}$,
∴k=-$\frac{1}{4}$,
∴抛物线解析式为y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$,
设过点P的直线为y=kx+b,把P(1,3)代入得3=k+b,
∴b=3-k,
∴过点P的直线为y=kx+3-k,
∵过点P的直线为y=kx+3-k与物线交于Q1(x1,y1)、Q2(x2,y2)两点,
∴y1=kx1+3-k,y2=kx2+3-k,
由$\left\{\begin{array}{l}{y=kx+3-k}\\{y=-\frac{1}{4}{x}^{2}+\frac{1}{2}x+\frac{15}{4}}\end{array}\right.$消去y得x2+(4k-2)x-3-4k=0,
∴x1+x2=-(4k-2),x1x2=-3-4k,
∴$\frac{{Q}_{1}P•{Q}_{2}P}{{Q}_{1}{Q}_{2}}$=$\frac{\sqrt{({x}_{1}-1)^{2}+({y}_{1}-3)^{2}}•\sqrt{({x}_{2}-1)^{2}+({y}_{2}-3)^{2}}}{\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}}$
=$\frac{(1+{k}^{2})•|({x}_{1}-1)({x}_{2}-1)|}{\sqrt{1+{k}^{2}}•|{x}_{1}-{x}_{2}|}$
=$\frac{(1+{k}^{2})•|{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1|}{\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}}$
=$\frac{(1+{k}^{2})•|-3-4k+4k-2+1|}{\sqrt{1+{k}^{2}}•\sqrt{16(1+{k}^{2})}}$
=1.
点评 本题考查二次函数综合题、抛物线与x轴的交点、两点间距离公式、一元二次方程的根与系数关系等知识,解题的关键是熟练应用根与系数关系,学会利用参数解决问题,本题化简有一定的难度,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
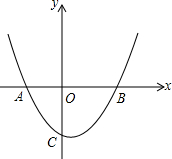 如图,二次函数图象经过A(-3,0)、B(4,0)、C(0,-4)三点.
如图,二次函数图象经过A(-3,0)、B(4,0)、C(0,-4)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
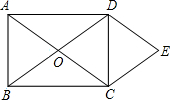 如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )
如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )| A. | 12cm2 | B. | 24cm2 | C. | 48cm2 | D. | 60cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com