
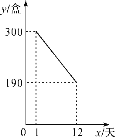
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
【答案】(1)240;(2)y=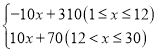 ;(3)9.5
;(3)9.5
【解析】
(1)由图像可得第12天的日销售量为190盒,因为从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒,故日销售量比第12天增加50盒,为240盒;
(2)当1≤x≤12时,令y=kx+b,代入x=1时,y=300;x=12,y=190即可求解;当12<x≤30时,则y=190+10(x-12),化简即可;
(3)先计算出当1≤x≤12时,有三天日销售利润不低于560元,确定当12<x≤30时,有三天日销售利润不低于560元,由函数的增减性即可求解.
(1)由图像可得第12天的日销售量为190盒,因为从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒,故日销售量比第12天增加50盒,为240盒;
故答案为:240
(2)当1≤x≤12时,
令y=kx+b.
由图知:当x=1时,y=300;x=12,y=190.
∴![]()
∴![]()
∴y=—10x+310(1≤x≤12).
当12<x≤30时,y=190+10(x-12).
∴y=10x+70 (12<x≤30).
∴y=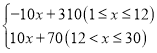
(3)当1≤x≤12时,
由(8-6)y≥560得, 2(-10x+310)≥560,
解得: x≤3.
∴1≤x≤3,x=1,2,3,共三天.
∵日销售利润不低于560元的天数共有6天,
∴当12<x≤30时,有三天日销售利润不低于560元,
由y=10x+70 (28<x≤30)得y随x的增大而增大,
∵x为整数,∴x=28,29,30时,日销售利润不低于560元,且当x=28时,利润最低.
由题意得,(8×0.1a-6)(10×28+70)≥560.
∴a≥9.5,
∴a的最小值为9.5.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
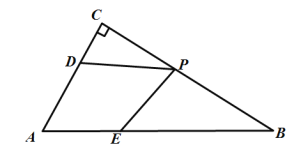
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,点D、E分别在边AC、AB上,AD=14,点P是边BC上一动点,当PD+PE的值最小时,AE=15,则BE为( )
A.30B.29C.28D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC为等腰直角三角形,AB=AC,△ADE为等腰直角三角形,AD=AE,点D在直线BC上,连接CE.
(1)判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;
(2)若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;
(3)若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象与直线
(x>0)的图象与直线![]() 相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.
相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若b=2![]() ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根;
②若方程ax2+bx+c=0有两个不等的实数根,则方程x2﹣bx+ac=0也一定有两个不等的实数根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则b2﹣4ac=(2ax0+b)2,其中正确的( )
A.只有①②③B.只有①②④C.①②③④D.只有③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 不与所在线段端点重合),
不与所在线段端点重合),![]() ,连接
,连接![]() ,射线
,射线![]() ,延长
,延长![]() 交射线
交射线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
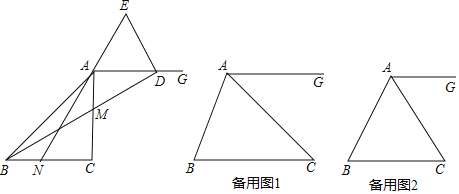
(1)如图,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 的关系:_____;
的关系:_____;![]() 与
与![]() 的位置关系:_____.
的位置关系:_____.
(2)当![]() ,其他条件不变时,
,其他条件不变时,![]() 的度数是多少?(用含
的度数是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=![]() 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=![]() 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com