
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
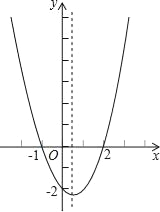
A. 函数有最小值 B. 对称轴是直线x=![]()
C. 当﹣1<x<2时,y<0 D. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
科目:初中数学 来源: 题型:
【题目】已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由;
(2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;
(3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
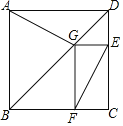
A.3100B.4600C.3000D.3600
查看答案和解析>>
科目:初中数学 来源: 题型:
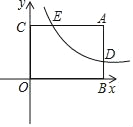
【题目】如图所示,已知矩形ABOC中,AC=4,双曲线y=![]() 与矩形两边AB、AC分别交于D、E,E为AC边中点.
与矩形两边AB、AC分别交于D、E,E为AC边中点.
(1)求点E的坐标;
(2)点P是线段OB上的一个动点,是否存在点P,使∠DPC=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
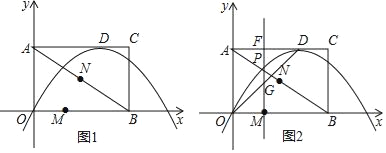
【题目】如图所示,在平面直角坐标系中,矩形AOBC的两边与坐标轴重合,且OB=4,AO=3,若AD=3DC,以D为顶点的抛物线过原点.点M、N为动点,设运动时间为t秒.
(1)求抛物线的解析式;
(2)在图1中,若点M在线段OB上从点O向点B以1个单位/秒的速度运动,同时,点N在线段BA上从点B向点A以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△BMN为直角三角形?
(3)在图2中,过点M做y轴的平行线,分别交抛物线和线段OD于P、G两点,当t为何值时,△ODP的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
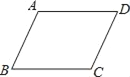
【题目】如图,已知ABCD.
(1)用直尺和圆规在BC边上取一点E,使AB=AE,连结AE;(保留作图痕迹,不写作法)
(2)在(1)的前提下,求证:AE=CD;∠EAD=∠D;
(3)若点E为BC的中点,连接BD,交AE于F,直接写出EF:FA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某班40名学生立定跳远的得分记录:
2,4,3,5,3,5,4,4,3,5
1,5,3,3,2,4,3,5,4,4
4,5,2,3,2,5,4,5,2,3
4,4,3,5,2,4,5,4,3,4
(1)完成下列统计表
得分 | 记录 | 人数 | 百分率% |
1 | |||
2 | |||
3 | |||
4 | |||
5 |
(2)用条形统计图表示上面的数据;
(3)用扇形统计图表示不同得分的同学人数占班级总人数的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
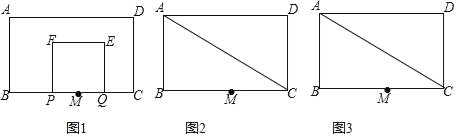
【题目】如图,在矩形ABCD中,AB=3,BC=4,点M是BC的中点,点P从点M出发沿MB以每秒1个单位的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;同时点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时,则两点停止运动,设点P,Q运动的时间是t秒(t>0).
(1)当点P运动到BM的中点时,t= ;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,直接写出S与t之间的函数关系式及t的取值范围;
(3)连结AC,当正方形PQEF与△ADC重叠部分为三角形时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
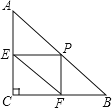
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是( )
![]()
A. 2B. 3C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com