
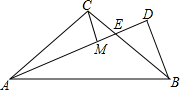
 如图,Rt△ABC中,AC=BC,∠ACB=90°,若AE为∠BAC的角平分线,BD⊥AE,垂足为D.
如图,Rt△ABC中,AC=BC,∠ACB=90°,若AE为∠BAC的角平分线,BD⊥AE,垂足为D.分析 (1)如图1中,延长AC交BD的延长线于H.首先证明△ACE≌△BCH,推出AE=BH,再证明DH=DB即可解决问题.
(2)如图2中,延长CM交AB于F,在AM上取一点H,使得MH=ME,首先证明CM=MF,再证明△ACH≌△CBF即可解决问题.
解答 证明:(1)如图1中,延长AC交BD的延长线于H.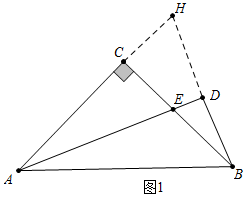
∵∠ACE=∠BDE=90°,∠AEC=∠BED,
∴∠CAE=∠EBD,
在△ACE和△BCH中,
$\left\{\begin{array}{l}{∠ACE=∠BCH=90°}\\{AC=BC}\\{∠CAE=∠CBH}\end{array}\right.$,
∴△ACE≌△BCH,
∴AE=BH,
∵∠DAH=∠DAB,∠DAH+∠H=90°,∠DAB+∠ABD=90°,
∴∠H=∠ABD,
∴AH=AB,∵AD⊥BH,
∴BD=DH,
∴AE=2BD.
(2)如图2中,延长CM交AB于F,在AM上取一点H,使得MH=ME.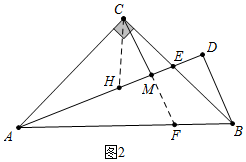
∵CM⊥AD,
∴∠AMC=∠AMF=90°,
∵∠MAC=∠MAF,∠MAC+∠ACM=90°,∠MAF+∠AFM=90°,
∴∠AFM=∠ACM,
∴AC=AF,∵AM⊥CF,
∴CM=MF,
∵CM⊥EH,MH=ME,
∴CH=AE,
∴∠AEH=∠CHE,
∵∠MCE+∠MEC=90°,∠CAE+∠AEC=90°,
∴∠MCE=∠CAE=∠FAM,
∵∠CME=∠AMF,
∴∠AFM=∠CEM=∠CHE,
∴∠AHC=∠CFB,
在△ACH和△CBF中,
$\left\{\begin{array}{l}{∠CAH=∠BCF}\\{∠AHC=∠CFB}\\{AC=BC}\end{array}\right.$,
∴△ACH≌△CBF,
∴AH=CF=2CM.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、等腰三角形的判定和性质、角平分线的定义等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题,属于中考常考题型.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
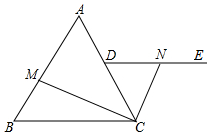 如图,在边长为6的等边△ABC中,D为AC中点,射线DE∥BC,M,N分别为线段AB与射线DE上的点,连结CM,CN,若BM=DN,则CM+CN的最小值为3$\sqrt{7}$.
如图,在边长为6的等边△ABC中,D为AC中点,射线DE∥BC,M,N分别为线段AB与射线DE上的点,连结CM,CN,若BM=DN,则CM+CN的最小值为3$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,对角线AC,BD交于点O,现有一块足够大的直角三角板的直角顶点与点O重合,当直角三角板绕着点O旋转时,两条直角边OP、OQ分别保持与边AB、边BC相交于点E、F,连结EF,下列结论:①EF=OB,②EF=$\sqrt{2}$OF;③当EF∥AC时,△BEF的周长最小;④当BE变化时,四边形OEBF的面积也随之变化.其中结论正确的个数为( )
如图,在正方形ABCD中,对角线AC,BD交于点O,现有一块足够大的直角三角板的直角顶点与点O重合,当直角三角板绕着点O旋转时,两条直角边OP、OQ分别保持与边AB、边BC相交于点E、F,连结EF,下列结论:①EF=OB,②EF=$\sqrt{2}$OF;③当EF∥AC时,△BEF的周长最小;④当BE变化时,四边形OEBF的面积也随之变化.其中结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将矩形ABCD纸片对折,设折痕为MN,再通过折叠使B点落在折线段MN上的B',设两条线段的交点为F,连接BF、EB'、FB'、AB'.
如图,将矩形ABCD纸片对折,设折痕为MN,再通过折叠使B点落在折线段MN上的B',设两条线段的交点为F,连接BF、EB'、FB'、AB'.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,AE=DE,AC与BD相交于点E,∠ADB=60°,且BE:ED=3:1,BD=12,求梯形ABCD的周长.
如图,在梯形ABCD中,AD∥BC,AE=DE,AC与BD相交于点E,∠ADB=60°,且BE:ED=3:1,BD=12,求梯形ABCD的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com