
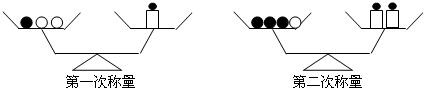
分析 设每只黑球的质量为x克,每只白球的质量为y克,根据“1只黑球、2只白球的总质量为5克,3只黑球、1只白球的总质量为10克”即可得出关于x、y的二元一次方程组,解之即可得出结论.
解答 解:设每只黑球的质量为x克,每只白球的质量为y克,
根据题意得:$\left\{\begin{array}{l}{x+2y=5}\\{3x+y=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$.
答:每只黑球的质量为3克,每只白球的质量为1克.
点评 本题考查了二元一次方程组的应用,根据天平两边的质量相当列出关于x、y的二元一次方程组是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2017 | B. | 2018 | C. | 20172 | D. | 20182 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=12}\\{5x+8y=1500}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x+\frac{2}{15}y=1.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+8y=1.5}\\{x+y=12}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x-\frac{2}{15}y=1.5}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
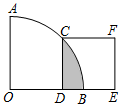 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | 2π-2 | C. | 4π-4 | D. | 4π-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com