
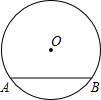
 如图半径为6的⊙O中,弦AB=8,则圆心O到AB的距离为2$\sqrt{5}$.
如图半径为6的⊙O中,弦AB=8,则圆心O到AB的距离为2$\sqrt{5}$.  新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 实验与探究:三角点阵前n行的点数计算.
实验与探究:三角点阵前n行的点数计算.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
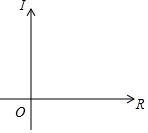 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:| R | … | 2 | 4 | 8 | 10 | 16 | … |
| I | … | 16 | 8 | 4 | 3.2 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
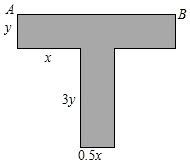 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
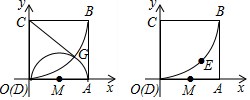 如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.
如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com