练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若一个三角形 三个内角度数的比为2︰7︰4，那么这个三角形是（   ）

    A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形

    C

    解析试题分析：∵一个三角形 三个内角度数的比为2︰7︰4，而三个内角度数之和为180度；∴这个三角形最大的角=；所以它是钝角三角形
    考点：判断三角形的形状
    点评：考察三角形形状的判定，解决本题的关键是考生对三角形形状的判定方法要熟练

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
    （1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；
    （2）在△ABC中，∠A＜∠B＜∠C．
    ①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；
    ②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•上城区二模）如图①，P为△ABC内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．已知△ABC中，∠A＜∠B＜∠C．
    （1）利用直尺和圆规，在图②中作出△ABC的自相似点P（不写作法，但需保留作图痕迹）；
    （2）若△ABC的三内角平分线的交点P是该三角形的自相似点，求该三角形三个内角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2011•南京）如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
    （1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；
    （2）在△ABC中，∠A＜∠B＜∠C．
    ①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；
    ②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．

    查看答案和解析>>

    科目：初中数学 来源：2012届浙江省杭州市上城区中考二模数学试卷（带解析） 题型：解答题

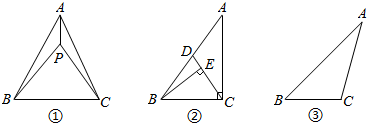
    如图①，P为△ABC内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
    已知△ABC中，∠A＜∠B＜∠C
    （1）利用直尺和圆规，在图②中作出△ABC的自相似点P（不写作法，但需保留作图痕迹）；
    （2）若△ABC的三内角平分线的交点P是该三角形的自相似点，求该三角形三个内角的度数．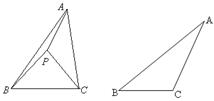

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年浙江省杭州市上城区中考二模数学试卷（解析版） 题型：解答题

     如图①，P为△ABC内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．

    已知△ABC中，∠A＜∠B＜∠C

    （1）利用直尺和圆规，在图②中作出△ABC的自相似点P（不写作法，但需保留作图痕迹）；

    （2）若△ABC的三内角平分线的交点P是该三角形的自相似点，求该三角形三个内角的度数．

     

    查看答案和解析>>

    同步练习册答案