
分析 (1)根据点(0,-3)在抛物线C1上,即可得出a的值,将其代入抛物线解析式中,再根据根与系数的关系找出x1+x2=-b、x1•x2=-3,结合|x1-x2|=4即可求出b的值,将其代入抛物线解析式中,利用配方法即可得出抛物线C1的顶点坐标;
(2)由x>0.利用配方法可得出x+$\frac{1}{x}$-2=$(\sqrt{x}-\frac{1}{\sqrt{x}})^{2}$,再根据偶次方非负可得出x+$\frac{1}{x}$≥2,并能找出当x=1时取等号;
(3)根据平移的性质找出抛物线C2的解析式,从而可找出A、B点的坐标,根据△AOB为直角三角形结合勾股定理找出m、n之间的关系,再根据三角形的面积公式即可找出S关于m的关系式,根据(2)的结论即可得出S的最小值,找出此时的点A的坐标即可得出一次函数OA的函数解析式.
解答 解:(1)∵抛物线过(0,-3)点,
∴-3a=-3,
∴a=1,
∴y=x2+bx-3.
∵x2+bx-3=0的两根为x1,x2且|x1-x2|=4,
∴x1+x2=-b,x1•x2=-3,
∴$|{{x_1}-{x_2}}|=\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{(-b)^{2}-4×(-3)}$=4且b<0,
∴b=-2,
∴y=x2-2x-3=(x-1)2-4,
∴抛物线C1的顶点坐标为(1,-4).
(2)∵x>0,
∴x+$\frac{1}{x}$-2=$(\sqrt{x}-\frac{1}{\sqrt{x}})^{2}$≥0,
∴$x+\frac{1}{x}≥2$,
显然当x=1时,才有$x+\frac{1}{x}=2$.
(3)由平移知识可得抛物线C2的解析式为:y=x2,
∴A(m,m2),B(n,n2),
∵△AOB为Rt△,
∴OA2+OB2=AB2,
∴m2+m4+n2+n4=(m-n)2+(m2-n2)2,
化简得:mn=-1,
∵S=$\frac{1}{2}OA•OB$=$\frac{1}{2}\sqrt{{m^2}+{m^4}}•\sqrt{{n^2}+{n^4}}$=$\frac{1}{2}$$\sqrt{{m}^{2}{n}^{2}+{m}^{2}{n}^{4}+{m}^{4}{n}^{2}+{m}^{4}{n}^{4}}$,
∵mn=-1,
∴S=$\frac{1}{2}\sqrt{2+{m^2}+{n^2}}=\frac{1}{2}\sqrt{2+{m^2}+\frac{1}{m^2}}$=$\frac{1}{2}\sqrt{{{(m+\frac{1}{m})}^2}}=\frac{1}{2}({m+\frac{1}{m}})≥\frac{1}{2}•2=1$,
∴S的最小值为1,此时m=1,A(1,1),
∴直线OA的一次函数解析式为y=x.
点评 本题考查了二次函数图象上点的坐标特征、根与系数的关系以及二次函数的性质,解题的关键是:(1)求出a、b值;(2)根据偶次方非负得出x+$\frac{1}{x}$≥2;(3)找出S关于m的函数关系式.本题属于中档题,难道不大,解决该题型题目时,巧妙利用x+$\frac{1}{x}$≥2是关键.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
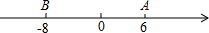 已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度变为M点的3倍.
已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度变为M点的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-3 | B. | m≥-3 | C. | m>-3且m≠$\frac{1}{2}$ | D. | m≥-3且m≠$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
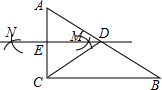 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )| A. | AD=CD | B. | ∠A=∠DCE | C. | ∠ADE=∠DCB | D. | ∠A=2∠DCB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com