
【题目】如图,矩形OABC的顶点A、C分别在![]() 的正半轴上,点B的坐标为(3,4)一次函数
的正半轴上,点B的坐标为(3,4)一次函数![]() 的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是![]() 轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.

【答案】(1)![]() ;
;
(2)M(1, ![]() );
);
(3)当四边形OMDN是菱形时,M(![]() ,
,![]() )N(
)N(![]() ,
,![]() )
)
【解析】分析:(1)首先在一次函数的解析式中令x=0,即可求得D的坐标,则OD的长度即可求得,OD=b,则E的坐标即可利用b表示出来,然后代入一次函数解析式即可得到关于b的方程,求得b的值;(2)首先求得四边形OAED的面积,则△ODM的面积即可求得,设出M的横坐标,根据三角形的面积公式即可求得M的横坐标,进而求得M的坐标;(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论,四边形OMDN是菱形时,M是OD的中垂线与DE的交点,M关于OD的对称点就是N;四边形OMND是菱形,OM=OD,M在直角DE上,设出M的坐标,根据OM=OD即可求得M的坐标,则根据ON和DM的中点重合,即可求得N的坐标.
本题解析:(1)y=![]() x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,
x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,
∵OD=BE,
∴BE=b,则E的坐标是(3,4b),
把E的坐标代入y=![]() x+b得4b=2+b,
x+b得4b=2+b,
解得:b=3;
(2) ![]() ,
,
∵三角形ODM的面积与四边形OAEM的面积之比为1:3,
∴![]() .
.
设M的横坐标是a,则![]() ×3a=1.5,解得:a=1,
×3a=1.5,解得:a=1,
把x=a=1代入y=![]() x+3得y=
x+3得y=![]() ×
×![]() +3=
+3=![]() .
.
则M的坐标是(1, ![]() );
);
(3)当四边形OMDN是菱形时,如图(1),M的纵坐标是![]() ,把y=
,把y=![]() 代入y=
代入y=![]() x+3,得
x+3,得![]() x+3=
x+3=![]() ,解得:x=
,解得:x=![]() ,
,
则M的坐标是(![]() ,
,![]() ),
),
则N的坐标是(![]() ,
,![]() );
);
当四边形OMND是菱形时,如图(2)OM=OD=3,设M的横坐标是m,则纵坐标是![]() m+3,则
m+3,则![]() ,
,
解得:m=![]() 或0(舍去).
或0(舍去).
则M的坐标是(![]() ,
,![]() ).
).
则DM的中点是(![]() ,
,![]() ).
).
则N的坐标是(![]() ,
,![]() ).
).
故N的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
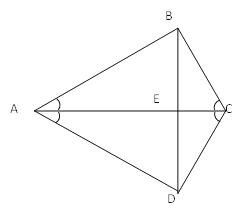
【题目】如图,
(1)如果,AC垂直平分BD.那么,CA平分∠BAD吗?CA平分∠BCD吗?
(2)如果,CA平分∠BAD,且CB⊥AB,CD⊥AD.那么,AC垂直平分BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com