
【题目】已知代数式![]() (n≠-2).
(n≠-2).
(1)①用含n的代数式表示m;
②若m、n均取整数,求m、n的值.
(2)当n取a、b时,m对应的值为c、d. 当-2<b<a时,试比较c、d的大小.
科目:初中数学 来源: 题型:
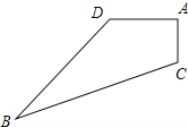
【题目】已知某实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草坪,经测量∠A=90°,AC=3m,BD=12m,CB=13m,DA=4m,若每平方米草坪需要300元,间学校需要投入多少资金买草坪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
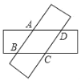
A.5 cmB.4.8 cmC.4.6 cmD.4 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求解一元一次方程,需要根据等式的基本性质,把方程转化为x=a的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,需要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为两个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解,各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想﹣转化,即把未知转化为已知来求解.
用“转化“的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程x3+x2﹣2x=0,通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得原方程x3+x2﹣2x=0的解.
再例如,解根号下含有来知数的方程:![]() =x,通过两边同时平方把它转化为2x+3=x2,解得:x1=3,x2=﹣1.因为2x+3≥0,且x≥0,所以x=﹣1不是原方程的根,x=3是原方程的解.
=x,通过两边同时平方把它转化为2x+3=x2,解得:x1=3,x2=﹣1.因为2x+3≥0,且x≥0,所以x=﹣1不是原方程的根,x=3是原方程的解.
(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)拓展:求方程![]() =x﹣1的解;
=x﹣1的解;
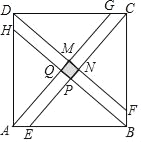
(3)应用:在一个边长为1的正方形中构造一个如图所示的正方形;在正方形ABCD边上依次截取AE=BF=CG=DH=![]() ,连接AG,BH,CE,DF,得到正方形MNPQ,若小正方形MNPQ(图中阴影部分)的边长为
,连接AG,BH,CE,DF,得到正方形MNPQ,若小正方形MNPQ(图中阴影部分)的边长为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=-![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C,两条直线l1、l2相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C,两条直线l1、l2相交于点D,连接AB.
(1)求两直线l1、l2交点D的坐标;
(2)求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.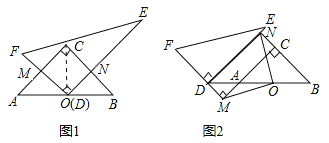
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com