练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在如图，在△ABC中，∠BAC＝90°，AB＝4 cm，AC＝6 cm，AM是中线．

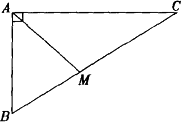
    (1)以点A为圆心，以4 cm长为半径作⊙A，则点B、C、M与⊙A的位置关系如何？

    (2)若以点A为圆心作⊙A，使B、C、M三点中至少有一点在圆内，且至少有一点在圆外，则⊙A的半径r的取值范围是什么？

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH：AC=2：3
    （1）延长HF交AB于G，求△AHG的面积．
    （2）操作：固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止，设运动的时间为t秒，运动后的直角梯形为DEFH′（如图）．
    探究1：在运动中，四边形CDH′H能否为正方形？若能，请求出此时t的值；若不能，请说明理由．
    探究2：在运动过程中，△ABC与直角梯形DEFH′重叠部分的面积为y，求y与t的函数关系．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•南平）如图，在△ABC中，点D、E分别在边BC、AC上，连接AD、DE，且∠1=∠B=∠C．
    （1）由题设条件，请写出三个正确结论：（要求不再添加其他字母和辅助线，找结论过程中添加的字母和辅助线不能出现在结论中，不必证明）
    答：结论一：
    AB=AC
    AB=AC
    ；
    结论二：
    ∠AED=∠ADC
    ∠AED=∠ADC
    ；
    结论三：
    △ADE∽△ACD
    △ADE∽△ACD
    ．
    （2）若∠B=45°，BC=2，当点D在BC上运动时（点D不与B、C重合），
    ①求CE的最大值；
    ②若△ADE是等腰三角形，求此时BD的长．
    （注意：在第（2）的求解过程中，若有运用（1）中得出的结论，须加以证明）

    查看答案和解析>>

    科目：初中数学 来源：2013年辽宁省辽阳市高级中等学校招生考试数学 题型：044

    定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”

    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等，

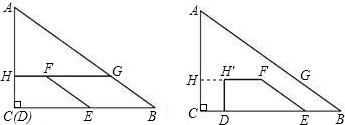
    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD＝S△BCD．

    应用：如图②，在矩形ABCD中，AB＝4，BC＝6，点E在AD上，点F在BC上，AE＝BF，AF与BE交于点O，

    (1)求证：△AOB和△AOE是“友好三角形”；

    (2)连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积，

    探究：在△ABC中，∠A＝30°，AB＝4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH：AC=2：3
    （1）延长HF交AB于G，求△AHG的面积．
    （2）操作：固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止，设运动的时间为t秒，运动后的直角梯形为DEFH′（如图）．
    探究1：在运动中，四边形CDH′H能否为正方形？若能，请求出此时t的值；若不能，请说明理由．
    探究2：在运动过程中，△ABC与直角梯形DEFH′重叠部分的面积为y，求y与t的函数关系．

    查看答案和解析>>

    科目：初中数学 来源：江苏期中题 题型：解答题

    如图，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH：AC=2：3
    （1）延长HF交AB于G，求△AHG的面积．
    （2）操作：固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止，设运动的时间为t秒，运动后的直角梯形为DEFH′（如图）．
    探究1：在运动中，四边形CDH?H能否为正方形？若能，请求出此时t的值；若不能，请说明理由．
    探究2：在运动过程中，△ABC与直角梯形DEFH?重叠部分的面积为y，求y与t的函数关系．

    查看答案和解析>>

    同步练习册答案