
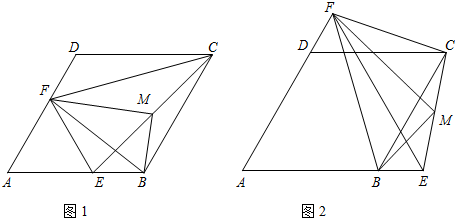
分析 (1)根据已知和菱形的性质证明△CBE≌△CDF,得到BE=DF,证明△AEF是等边三角形,求出EF的长;
(2)延长BM交DC于点N,连结FN,证明△CMN≌△EMB,得到NM=MB,证明△FDN≌△BEF,得到FN=FB,得到BM⊥MF;
(3)延长BM交DC的延长线于点N,连结FN,与(2)的证明方法相似证明BM⊥MF.
解答 (1)解:∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠D=∠CBE,
又∵∠BCE=∠DCF,
∴△CBE≌△CDF,
∴BE=DF.
又∵AB=AD,∴AB-BE=AD-DF,即AE=AF,
又∵∠A=60°,∴△AEF是等边三角形,
∴EF=AF,
∵AF=1,∴EF=1.
(2)证明:如图1,延长BM交DC于点N,连结FN,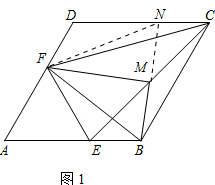
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,∴∠A+∠D=180°,
又∵∠A=60°,∴∠D=120°,
∴∠D=∠BEF.
又∵DN=EF,BE=DF.
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,∴BM⊥MF;
(3)结论BM⊥MF仍然成立.
证明:如图2,延长BM交DC的延长线于点N,连结FN,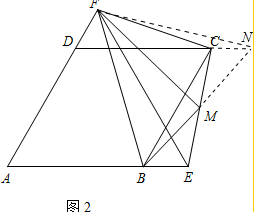
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,∴∠A+∠FDC=180°,
又∵∠A=60°,∴∠FDC=120°,
∴∠FDC=∠BEF.
又∵DN=EF,BE=DF.
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,
∴BM⊥MF.
点评 本题考查的是菱形的性质、全等三角形的判定和性质以及等腰三角形的性质,正确作出辅助线、构造全等三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
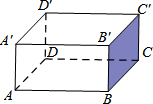 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )| A. | $\sqrt{53}$cm | B. | $\sqrt{45}$cm | C. | $\sqrt{41}$cm | D. | 7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 年级 | 七年级 | 八年级 | 九年级 |
| 学生人数 | 180 | 165 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com