
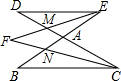
 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.分析 (1)根据EF为∠BED的平分线可得∠DEF=15°,由∠EMA=∠D+∠DEF,∠D=70°,可以求得∠EMA的度数;
(2)根据CF为∠BCD的平分线可得∠BCN=20°,由∠ENC=∠B+∠BCN,∠B=60°,可以求得∠ENC的度数;
(3)∠F=$\frac{1}{2}$(∠B+∠D),由三角形的外角等于和它不相邻的两个内角的和,三角形的角平分线的知识可以得到∠B,∠D,∠F三者之间的关系,从而证明结论.
解答 解:(1)∵EF为∠BED的平分线,∠BED=30°,
∴∠DEM=∠FEN=$\frac{1}{2}$∠BED=15°.
又∵∠EMA=∠D+∠DEM,∠D=70°,
∴∠EMA=85°.
故答案为:85°.
(2)∵CF为∠BCD的平分线,∠BCD=40°,
∴∠BCN=∠FCM=$\frac{1}{2}$∠BCD=20°.
又∵∠ENC=∠B+∠BCN,∠B=60°,
∴∠ENC=80°.
故答案为:80°.
(3)∠F=$\frac{1}{2}$(∠B+∠D).
证明:∵∠EMA=∠D+∠DEF=∠F+∠DCF,
∠ENC=∠B+∠BCF=∠F+∠BEF,
∴∠D+∠DEF+∠B+∠BCF=∠F+∠DCF+∠F+∠BEF.
又∵CF为∠BCD的平分线,EF为∠BED的平分线,
∴∠DEF=∠BEF,∠DCF=∠BCF.
∴∠B+∠D=2∠F.
即:∠F=$\frac{1}{2}$(∠B+∠D).
点评 本题主要考查三角形角平分线和三角形的外角的知识,关键是明确三角形的外角等于和它不相邻的两个内角的和,进行灵活变化,证明出相应的结论.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y=-x2-2x+3.
已知函数y=-x2-2x+3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}>-\frac{1}{3}$ | B. | -|-1|>-|+1| | C. | $-\frac{4}{5}<-\frac{5}{6}$ | D. | $|{-\frac{1}{2}}|>|{-\frac{1}{3}}|$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
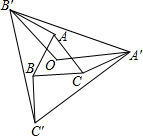 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com