
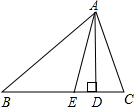
 如图,已知△ABC,∠C=70°,∠B=40°,AD⊥BC,AE平分∠BAC,则∠DAE=15°.
如图,已知△ABC,∠C=70°,∠B=40°,AD⊥BC,AE平分∠BAC,则∠DAE=15°. 分析 在△ABC中利用三角形内角和定理即可得出∠BAC的度数,根据角平分线的定义即可求出∠BAE的度数,再在△BAD中利用三角形内角和定理可求出∠BAD的度数,由∠DAE=∠BAD-∠BAE,代入数据即可得出结论.
解答 解:在△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°-∠B-∠C=70°,
∴AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=35°.
在△BAD中,∠B=40°,AD⊥BC,
∴∠BDA=90°,∠BAD=180°-∠B-∠BDA=50°,
∴∠DAE=∠BAD-∠BAE=50°-35°=15°.
故答案为:15°.
点评 本题考查了三角形内角和定理,根据三角形内角和定理求出∠BAC和∠BAD的度数是解题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
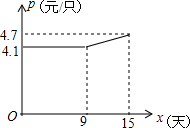 某企业接到一批月饼生产任务,按要求在15天内完成,约定这批月饼的出厂价为每块6元,为按时完成任务,该企业招收了新工人.设新工人王红第x天生产的月饼数量为y块,y与x满足下列关系式:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5≤x≤15)}\end{array}\right.$.
某企业接到一批月饼生产任务,按要求在15天内完成,约定这批月饼的出厂价为每块6元,为按时完成任务,该企业招收了新工人.设新工人王红第x天生产的月饼数量为y块,y与x满足下列关系式:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5≤x≤15)}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com