
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A( ,﹣2),反比例函数y=
,﹣2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(1)y=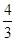 x﹣4;(2)(
x﹣4;(2)(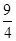 ,﹣1).
,﹣1).
解析试题分析:(1)由A为直角三角形外心,得到A为斜边MN中点,根据A坐标确定出M与N坐标,设直线l解析式为y=mx+n,将M与N坐标代入求出m与n的值,即可确定出直线l解析式;
(2)将A坐标代入反比例解析式求出k的值,确定出反比例解析式,利用反比例函数k的意义求出△OBC的面积,由△ONP的面积是△OBC面积的3倍求出△ONP的面积,确定出P的横坐标,即可得出P坐标.
试题解析:(1)∵Rt△MON的外心为点A( ,﹣2),
,﹣2),
∴A为MN中点,即M(3,0),N(0,﹣4),
设直线l解析式为y=mx+n,
将M与N代入得: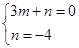 ,
,
解得:m=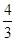 ,n=﹣4,
,n=﹣4,
则直线l解析式为y=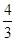 x﹣4;
x﹣4;
(2)将A( ,﹣2)代入反比例解析式得:k=﹣3,
,﹣2)代入反比例解析式得:k=﹣3,
∴反比例解析式为y=﹣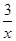 ,
,
∵B为反比例函数图象上的点,且BC⊥x轴,
∴S△OBC= ,
,
∵S△ONP=3S△OBC,
∴S△ONP=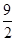 ,
,
设P横坐标为a(a>0),
∴ ON•a=3×
ON•a=3× ,即a=
,即a=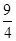 ,
,
则P坐标为(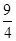 ,﹣1).
,﹣1).
【考点】反比例函数综合题.


科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
⑴求k的值;
⑵若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=x+1与y轴交于A点,与反比列函数y= (x>0)的图象交于点M,过M作MH⊥x,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x,且tan∠AHO= .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数y= (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
我们规定:形如 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当 时,“奇特函数”
时,“奇特函数” 就是反比例函数
就是反比例函数 .
.
(1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”;
(2) 如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3).点D是OA的中点,连结OB,CD交于点E,“奇特函数” 的图象经过B,E两点.
的图象经过B,E两点.
① 求这个“奇特函数”的解析式;
② 把反比例函数 的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为
的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为 ,请直接写出点P的坐标.
,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示是某一蓄水池的排水速度 h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
h)与排完水池中的水所用的时间t(h)之间的函数关系图象. 
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量是 ,那么水池中的水要用多少小时排完?
,那么水池中的水要用多少小时排完?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com