【题目】下列二次函数中有一个函数的图像与x轴有两个不同的交点，这个函数是（ ）
A. 
B. 
C. 
D. 
科目：初中数学 来源： 题型：
【题目】把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4 cm，则球的半径长是（ ）
A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请阅读下列材料，并完成相应的任务．
在数学中，当问题的条件不够时间，常添加辅助线构成新图形，形成新关系，建立已知与未知的桥梁，从而把原问题转化为易于解决的问题．在著名美籍匈牙利数学教波利亚所著的《数学的发现》一书中有这样一个例子：试作一个三角形，使它的三边长分别是各条中线长的三分之一，解决这个问题的步骤如下：
第一步，如图1，己知
的三条中线
，
和
相交于点
，则有
．
下面是该结论的部分证明过程：
证明：如图1，过点
作的平分线，交的延长线于点
，则
．
又
，
∴
．
∴
．
∵点
是
的中点，
∴
．
……
第二步，同理可以证明：
．
第三步，如图2，取BM的中点
，连接
.则
的三边长分别是各条中线长的三分之一．
任务：（1）请在上面第一步中证明过程的基础上完成对结论的证明；
（2）请完成第三步的结论的证明；
（3）请直接写出图2中
与的面积比：
_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA＝2，OB＝1，斜边AC∥x轴．若反比例函数y
（k＞0，x＞0）的图象经过AC的中点D，则k的值为（ ）
A.4B.5C.6D.8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图Rt△ABC中，∠ACB＝90°，AC＝4，BC＝2，点P在边AC上运动（点P与点A、C不重合）．以P为圆心，PA为半径作⊙P交边AB于点D、过点D作⊙P的切线交射线BC于点E（点E与点B不重合）．
（1）求证：BE＝DE；
（2）若PA＝1．求BE的长；
（3）在P点的运动过程中．（BE+PA）PA的值是否有最大值？如果有，求出最大值；如果没有，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
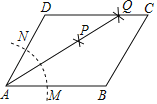
【题目】如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于
MN的长为半径作弧，两弧相交于点P；③作AP射线，交边CD于点Q，若DQ=2QC，BC=3，则平行四边形ABCD周长为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
（
为正整数，且
）与
轴的交点为
和
，
，当
时，第1条抛物线
与轴的交点为和
，其他依次类推．
（1）求
，
的值及抛物线
的解析式；
（2）抛物线
的顶点
的坐标为（ ， ）；依次类推，第
条抛物线
的顶点
的坐标为（ ， ）；所有抛物线的顶点坐标满足的函数关系式是 ；
（3）探究下列结论：
①是否存在抛物线，使得
为等腰直角三角形？若存在，请求出抛物线的表达式；若不存在，请说明理由；
②若直线
与抛物线分别交于则线段
，
，…
则线段
，
，…
的长有何规律？请用含
的代数式表示．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
