
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{3}{2}$ |
分析 根据x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,可以求得(1+$\frac{1}{y}$)(1-$\frac{1}{x}$)的值,本题得以解决.
解答 解:∵x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,
∴(1+$\frac{1}{y}$)(1-$\frac{1}{x}$)
=(1+$\frac{1}{\sqrt{3}-1}$)(1-$\frac{1}{\sqrt{3}+1}$)
=(1+$\frac{\sqrt{3}+1}{2}$)(1-$\frac{\sqrt{3}-1}{2}$)
=1-$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{3}+1}{2}$-$\frac{1}{2}$
=$\frac{3}{2}$,
故选D.
点评 本题考查分式的混合运算,解题的关键是明确分式的混合运算的计算法,计算时要仔细认真.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
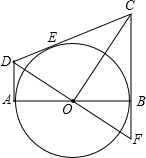 如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).
如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种消毒液(瓶) | 乙种消毒液(瓶) | 总费用(元) | |
| 第一次 | 40 | 60 | 660 |
| 第二次 | 80 | 30 | 690 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形中,AE⊥BC于E,AF⊥CD于F.
如图,平行四边形中,AE⊥BC于E,AF⊥CD于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com