
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | $\sqrt{27}$÷$\sqrt{3}$=3 | D. | 2$\sqrt{3}$×3$\sqrt{3}$=6 |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
 如图,已知a∥b,三角形的直角顶点在直线a上,已知∠1=25°18'27'',则∠2的度数是( )
如图,已知a∥b,三角形的直角顶点在直线a上,已知∠1=25°18'27'',则∠2的度数是( )| A. | 25°18'27'' | B. | 64° 41'33'' | C. | 74°41'33'' | D. | 64° 41'43'' |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
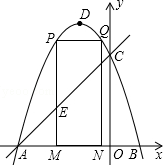 如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
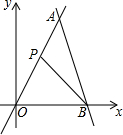 如图,在平面直角坐标系中,直线OA的函数表达式为y=2x,直线AB的函数表达式为y=-3x+b,点B的坐标为$(\frac{10}{3},0)$.点P沿折线OA-AB运动,且不与点O和点B重合.设点P的横坐标为m,△OPB的面积为S.
如图,在平面直角坐标系中,直线OA的函数表达式为y=2x,直线AB的函数表达式为y=-3x+b,点B的坐标为$(\frac{10}{3},0)$.点P沿折线OA-AB运动,且不与点O和点B重合.设点P的横坐标为m,△OPB的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×0.8-x=2 | B. | 12-x×0.8=2 | C. | (12-x)×0.8=2 | D. | 12-x=2×0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2 | B. | y=3 | C. | $\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com