
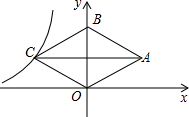
 如图,菱形OABC的顶点O是原点,顶点B在y轴上,已知菱形的边长为5,一条对角线的长是6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,则k的值为-12.
如图,菱形OABC的顶点O是原点,顶点B在y轴上,已知菱形的边长为5,一条对角线的长是6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,则k的值为-12. 分析 先根据菱形的性质以及勾股定理求出C点坐标,再把C点坐标代入反比例函数的解析式即可得出k的值.
解答 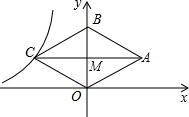 解:如图,设菱形两对角线交于点M,
解:如图,设菱形两对角线交于点M,
∵菱形的边长为5,一条对角线的长是6,
∴OC=5,OM=$\frac{1}{2}$OB=3,AC⊥OB.
在Rt△OCM中,∵∠OMC=90°,
∴CM=$\sqrt{O{C}^{2}-O{M}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴C(-4,3),
∵反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,
∴3=$\frac{k}{-4}$,
解得k=-12.
故答案为:-12.
点评 本题考查的是反比例函数图象上点的坐标特征,即反比例函数图象上各点的坐标一定满足此函数的解析式.也考查了菱形的性质以及勾股定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
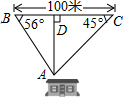 如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为60米.(sin56°≈0.8,tan56°≈1.5)
如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为60米.(sin56°≈0.8,tan56°≈1.5)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-m}$ | B. | -$\sqrt{m}$ | C. | -$\sqrt{-m}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com