
 小明同学将图(1)中的阴影部分(边长为m的大正方形中有一个边为n的小正方形)拼成了一个长方形(如图2),比较两个图的面积可以得出的结论是m2-n2=(m+n)(m-n) (用含m,n的式子表达)
小明同学将图(1)中的阴影部分(边长为m的大正方形中有一个边为n的小正方形)拼成了一个长方形(如图2),比较两个图的面积可以得出的结论是m2-n2=(m+n)(m-n) (用含m,n的式子表达)分析 根据题意分别求得(1)与(2)中阴影部分的面积,由两图形阴影面积相等,即可求得答案.
(1)利用平方差公式,即可解答;
(2)利用平方差公式,即可解答.
解答 解:根据题意得:
(1)中阴影部分的面积为:m2-n2;
(2)中阴影部分的面积为:(m+n)(m-n).
∵两图形阴影面积相等,
∴可以得到的结论是:m2-n2=(m-n)(m+n).
故答案为:m2-n2=(m-n)(m+n).
(1)20102-2009×2011
=20102-(2010-1)(2010+1)
=20102-20102+1
=1.
(2)(x-2y+1)(x+2y-1)
=[x-(2y-1)][x+(2y-1)]
=x2-(2y-1)2
=x2-4y2+4y-1.
点评 本题主要考查了平方差公式的几何表示,表示出图形阴影部分面积是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.
如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| y(单位:度) | 100 | 200 | 400 | 500 | … |
| x(单位:米) | 1.00 | 0.50 | 0.25 | 0.20 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
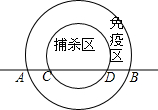 高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,若∠1=∠2,则AB∥CD,试判断命题的真假:假(填“真”或“假”).
(1)如图,若∠1=∠2,则AB∥CD,试判断命题的真假:假(填“真”或“假”).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com