
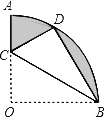
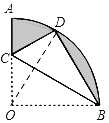
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,求图中阴影部分的面积.
【答案】![]()
【解析】
根据题意连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又在扇形OAB中,∠AOB=90°,半径OA=2,即可求得扇形OAB的面积,继而求得阴影部分面积.
解:连接OD.
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形
∴∠DBO=60°,
∴∠CBO=![]() ∠DBO=30°,
∠DBO=30°,
∵∠AOB=90°,
∴OC=OBtan∠CBO=2×![]() ,
,
∴S△BDC=S△OBC=![]() ×OB×OC=
×OB×OC=![]() ×2×
×2×![]() ,
,
S扇形AOB=![]() =π,
=π,
∴阴影部分的面积为:S扇形AOB﹣S△BDC﹣S△OBC=π﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
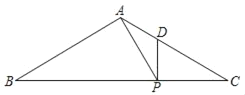
【题目】如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,![]() .
.
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
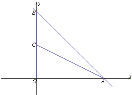
【题目】已知,平面直角坐标系中,直线y=-x+6交x轴于点A,交y轴于点B,点C为OB上一点,连接AC,且![]() ;
;
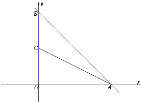
(1)求C点坐标;
(2)D为OC上一点,连接AD并延长至点E,连接OE、CE,取AE中点F,连接BF、OF,当F在第一象限时,求![]() 的值;
的值;
(3)在(2)的条件下,将射线AC延AE翻折交OE于点P,连接BP,过O作OH⊥AE于H,若AD=4FH,![]() ,求直线PB的解析式.
,求直线PB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:当
的坐标定义如下:当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 的变换点
的变换点![]() 的坐标是_________;点
的坐标是_________;点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() __________
__________![]() ;
;
(2)若点![]() 是函数
是函数![]() 图象上的一点,点
图象上的一点,点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,求线段
,求线段![]() 长的取值范围;
长的取值范围;
(3)已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .点
.点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 的变换点为
的变换点为![]() .若点
.若点![]() 恰好在抛物线的对称轴上,且四边形
恰好在抛物线的对称轴上,且四边形![]() 是菱形,求
是菱形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.

(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
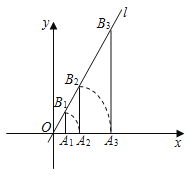
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交过原点与x轴夹角为60°的直线l于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3按此做法进行下去,则点B2019的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
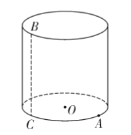
【题目】如图,在一圆柱铁桶内底面的点![]() 处有一飞虫,在其上边沿的点
处有一飞虫,在其上边沿的点![]() 处有一面包残渣,已知
处有一面包残渣,已知![]() 是点
是点![]() 正下方的桶内底面上一点,已知劣弧
正下方的桶内底面上一点,已知劣弧![]() 的长为
的长为![]() ,铁桶的底面直径为
,铁桶的底面直径为![]() ,桶高为60cm,则该飞虫从点
,桶高为60cm,则该飞虫从点![]() 到达
到达![]() 的最短路径是____________cm.
的最短路径是____________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com