
【题目】结合图形填空:
已知,如图,∠BAE+∠AED=180°,∠M=∠N,试说明:∠1=∠2.
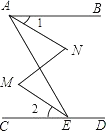
解:∵∠BAE+∠AED=180°
∴ AB∥CD( )
∴∠BAE= ( )
又∵∠M=∠N (已知)
∴ AN∥ ( )
∴∠NAE= (两直线平行,内错角相等)
∴∠BAE﹣∠NAE= ﹣
即∠1=∠2.( )
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,过点
,过点![]() 画
画![]() 轴的垂线
轴的垂线![]() ,点
,点![]() 在线段
在线段![]() 上,连结
上,连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,过点
,过点![]() 画
画![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求![]() 的度数,并直接写出直线
的度数,并直接写出直线![]() 的解析式;
的解析式;
(2)若点![]() 的横坐标为2,求
的横坐标为2,求![]() 的长;
的长;
(3)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
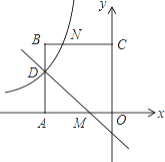
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OMP的面积等于2,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
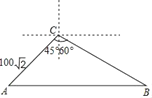
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
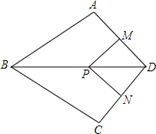
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和父母打算去某火锅店吃火锅,该店在网上出售“![]() 元抵
元抵![]() 元的全场通用代金券”(即面值
元的全场通用代金券”(即面值![]() 元的代金券实付
元的代金券实付![]() 元就能获得),店家规定代金券等同现金使用,一次消费最多可用
元就能获得),店家规定代金券等同现金使用,一次消费最多可用![]() 张代金券,而且使用代金券的金额不能超过应付总金额.
张代金券,而且使用代金券的金额不能超过应付总金额.
(1)如果小明一家应付总金额为![]() 元,那么用代金券方式买单,他们最多可以优惠多少元:
元,那么用代金券方式买单,他们最多可以优惠多少元:
(2)小明一家来到火锅店后,发现店家现场还有一个优惠方式: 除锅底不打折外,其余菜品全部![]() 折.小明一家点了一份
折.小明一家点了一份![]() 元的锅底和其他菜品,用餐完毕后,聪明的小明对比两种优惠,选择了现场优惠方式买单,这样比用代金券方式买单还能少付
元的锅底和其他菜品,用餐完毕后,聪明的小明对比两种优惠,选择了现场优惠方式买单,这样比用代金券方式买单还能少付![]() 元.问小明一家实际付了多少元?
元.问小明一家实际付了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a﹣b|.根据阅读材料与你的理解回答下列问题:
![]()
(1)数轴上表示3与﹣4两点之间的距离是 .
(2)数轴上有理数x与有理数8所对应两点之间的距离用绝对值符号可以表示为 .
(3)代数式|x+6|可以表示数轴上有理数x与有理数 所对应的两点之间的距离;若|x+6|=5,则x= .
(4)求代数式|x+1010|+|x+504|+|x﹣1009|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
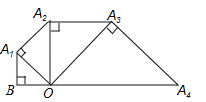
【题目】如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com