
【题目】某公司销售一种新型产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=-![]() x+150,成本为50元/件,无论销售多少,每月还需支出广告费90000元,设月利润为w内(元),若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10
x+150,成本为50元/件,无论销售多少,每月还需支出广告费90000元,设月利润为w内(元),若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10![]() a
a![]() 40),当月销量为x(件)时,每月还需缴纳
40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
【答案】(1)140,0(2)w内=-![]() x2+100x-90000,w外=-
x2+100x-90000,w外=-![]() x2+(150-a)x;(3)当x=5000时,在国内销售的月利润最大;a=34
x2+(150-a)x;(3)当x=5000时,在国内销售的月利润最大;a=34
【解析】
(1)将x=1000代入求值即可;
(2)根据“利润=销售额-成本-广告费”可求出![]() 与x间的函数关系式,根据“利润=销售额-成本-附加费”可求出
与x间的函数关系式,根据“利润=销售额-成本-附加费”可求出![]() 与x间的函数关系式;
与x间的函数关系式;
(3)先运用二次函数的性质求出![]() 取最大值时x的值,再根据
取最大值时x的值,再根据![]() 的最大值等于
的最大值等于![]() 的最大值,列出关于a的方程,解方程即可求出a的值.
的最大值,列出关于a的方程,解方程即可求出a的值.
解:(1)①![]()
②![]() ;
;
(2)w内=x(y-50)-90000=x(-![]() x+150-50)-90000=-
x+150-50)-90000=-![]() x2+100x-90000,
x2+100x-90000,
w外=x(150-a)-![]() x2=-
x2=-![]() x2+(150-a)x,
x2+(150-a)x,
(3)∵w内=-![]() x2+100x-90000,∴当x=-
x2+100x-90000,∴当x=- =5000时,w内最大;
=5000时,w内最大;
∵在国外销售月利润的最大值与在国内销售月利润的最大值相同,
∴ ,整理,得(150-a)2=13600,解得a1=34,a2=284(不合题意,舍去).∴a=34.
,整理,得(150-a)2=13600,解得a1=34,a2=284(不合题意,舍去).∴a=34.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
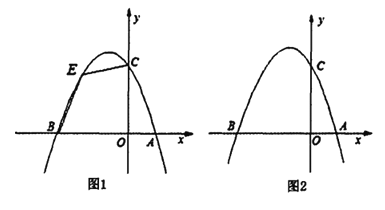
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(l)求抛物线的表达式;
(2)如图l,若点![]() 为第二象限抛物线上一动点,连接
为第二象限抛物线上一动点,连接![]() ,求四边形
,求四边形![]() 面积的最大值,并求此时
面积的最大值,并求此时![]() 点的坐标;
点的坐标;
(3)如图2,在![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() 为等腰三角形?若存在,请求出所有符合条件的点
为等腰三角形?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
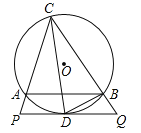
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点B的坐标为![]() ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数
,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数![]() 的图象交AB,BC分别于点E,F.
的图象交AB,BC分别于点E,F.

(1)求直线EF的解析式.
(2)求四边形BEOF的面积.
(3)若点P在y轴上,且![]() 是等腰三角形,请直接写出点P的坐标.
是等腰三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
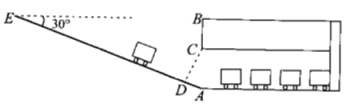
【题目】如下图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米.地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,则关于该函数的下列说法正确的是( )
,则关于该函数的下列说法正确的是( )
A.该函数图象与![]() 轴的交点坐标是
轴的交点坐标是![]()
B.当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小
值的增大而减小
C.当![]() 取
取![]() 和
和![]() 时,所得到的
时,所得到的![]() 的值相同
的值相同
D.将![]() 的图象先向左平移两个单位,再向上平移
的图象先向左平移两个单位,再向上平移![]() 个单位得到该函数图象
个单位得到该函数图象
查看答案和解析>>
科目:初中数学 来源: 题型:
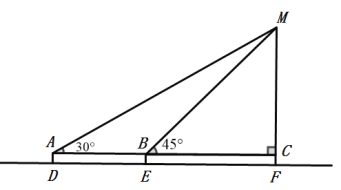
【题目】某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,请根据他们的测量数据求此楼MF的高(结果精确到0.1m,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com