
”¾ĢāÄæ”æij°ą¾ŁŠŠĢųÉž±ČČü£¬ČüŗóÕūĄķ²ĪČüѧɜµÄ³É¼Ø£¬½«Ń§Éś³É¼Ø·ÖĪŖA”¢B”¢C”¢DĖÄøöµČ¼¶£¬²¢½«½į¹ū»ęÖĘ³ÉČēĶ¼ĖłŹ¾µÄĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£¬µ«¾ł²»ĶźÉĘ£®
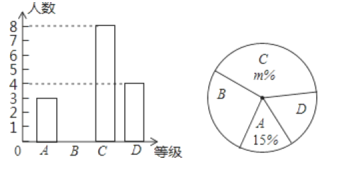
ĒėÄćøł¾ŻĶ³¼ĘĶ¼½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©²Ī¼Ó±ČČüµÄѧɜ¹²ÓŠ______Ćū£»
£Ø2£©ŌŚÉČÓ°Ķ³¼ĘĶ¼ÖŠ£¬mµÄÖµĪŖ_____£¬±ķŹ¾DµČ¼¶µÄÉČŠĪµÄŌ²ŠÄ½ĒĪŖ____¶Č£»
£Ø3£©ĻČ¾ö¶Ø“Ó±¾“Ī±ČČü»ńµĆBµČ¼¶µÄѧɜ֊£¬Ń”³ö2ĆūČ„²Ī¼ÓѧŠ£µÄÓĪŌ°»ī¶Æ£¬ŅŃÖŖBµČ¼¶Ń§ÉśÖŠÄŠÉśÓŠ2Ćū£¬ĘäĖū¾łĪŖÅ®Éś£¬ĒėÓĆĮŠ±ķ·Ø»ņ»Ź÷דĶ¼·ØĒó³öĖłŃ”2ĆūѧɜøųŗĆŹĒŅ»ĆūÄŠÉśŅ»ĆūÅ®ÉśµÄøÅĀŹ£®
”¾“š°ø”æ£Ø1£©20£»£Ø2£©40£¬72£»£Ø3£©![]()
”¾½āĪö”æ
£Ø1£©øł¾ŻµČ¼¶ĪŖAµÄČĖŹż³żŅŌĖłÕ¼µÄ°Ł·Ö±ČĒó³ö×ÜČĖŹż£»
£Ø2£©øł¾ŻD¼¶µÄČĖŹżĒóµĆDµČ¼¶ÉČŠĪŌ²ŠÄ½ĒµÄ¶ČŹżŗĶmµÄÖµ£»
£Ø3£©Ēó³öÅ®ÉśÓŠ3Ćū£¬ĮŠ±ķµĆ³öĖłÓŠµČæÉÄܵÄĒéæöŹż£¬ÕŅ³öŅ»ÄŠŅ»Å®µÄĒéæöŹż£¬¼“æÉĒó³öĖłĒóµÄøÅĀŹ£®
½ā£ŗ£Ø1£©3”Ā15%£½20£ØĆū£©£»
¹Ź“š°øĪŖ£ŗ20£»
£Ø2£©”ß8”Ā20£½40%£¬
”ąm£½40£»
±ķŹ¾DµČ¼¶µÄÉČŠĪµÄŌ²ŠÄ½ĒĪŖ£ŗ360”ć”Į![]() £½72”ć£»
£½72”ć£»
¹Ź“š°øĪŖ£ŗ40£¬72£»
£Ø3£©BµČ¼¶Ń§ÉśČĖŹżĪŖ20©3©8©4£½5£ØČĖ£©£¬
BµČ¼¶Ń§ÉśÖŠÄŠÉśÓŠ2Ćū£¬
ŌņÅ®ÉśÓŠ3Ćū£¬
»Ź÷דĶ¼ČēĶ¼£ŗ

¹²ÓŠ20øöµČæÉÄܵĽį¹ū£¬
ĖłŃ”2ĆūѧɜĒ”ŗĆŹĒŅ»ĆūÄŠÉśŅ»ĆūÅ®ÉśµÄ½į¹ūÓŠ12øö£¬
”ąĖłŃ”2ĆūѧɜĒ”ŗĆŹĒŅ»ĆūÄŠÉśŅ»ĆūÅ®ÉśµÄøÅĀŹĪŖ![]() £®
£®


 æŚĖćĢāæؼÓÓ¦ÓĆĢā¼ÆѵĻµĮŠ“š°ø
æŚĖćĢāæؼÓÓ¦ÓĆĢā¼ÆѵĻµĮŠ“š°ø ×ŪŗĻ×Ō²āĻµĮŠ“š°ø
×ŪŗĻ×Ō²āĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬EŹĒBCµÄÖŠµć£¬FŹĒCDÉĻŅ»µć£¬AE”ĶEF£®ÓŠĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻBAE£½”ĻEAF£»¢ŚÉäĻßFEŹĒ”ĻAFCµÄ½ĒĘ½·ÖĻߣ»¢ŪCF£½![]() CD£»¢ÜAF£½AB+CF£®ĘäÖŠÕżČ·½įĀŪµÄøöŹżĪŖ£Ø””””£©
CD£»¢ÜAF£½AB+CF£®ĘäÖŠÕżČ·½įĀŪµÄøöŹżĪŖ£Ø””””£©
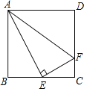
A.1øöB.2øöC.3øöD.4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2020ÄźĶ»ČēĘ䥓µÄ·ĪŃ×ŅßĒ飬øųĪŅĆĒµÄÉś»īŗĶѧĻ°“ųĄ“ĮĖÖī¶ą²»±ć£®Ķ¼1ŹĒ2ŌĀ1ČÕÖĮ2ŌĀ5ČÕČ«¹ś”°ŠĀ¹Ś·ĪŃ×”±ŅßĒéŠĀŌöŹż¾ŻĶ³¼ĘĶ¼£¬ĪŖĮĖæŲÖĘŅßĒéĀūŃÓĄ©É¢£¬¹ś¼ŅČ«ĆęĀ䏵ŅßĒé·ĄæŲ¹¤×÷£¬¾Ł¹śÉĻĻĀÖŚÖ¾³É³Ē£¬Ķ¼2ŹĒ3ŌĀ5ČÕÖĮ3ŌĀ9ČÕČ«¹ś”°ŠĀ¹Ś·ĪŃ×”±ŅßĒéŠĀŌöŹż¾ŻĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ³¼ĘĶ¼½ā“šŅŌĻĀĪŹĢā£ŗ
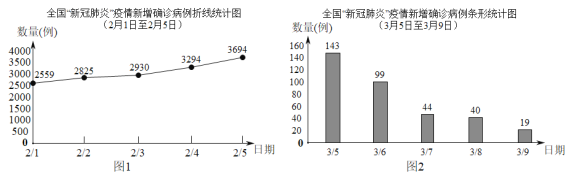
£Ø1£©Š“³ö2ŌĀ3ČÕČ«¹śŠĀŌöČ·Õļ²”ĄżŹż£¬²¢¼ĘĖć3ŌĀ5ČÕÖĮ3ŌĀ9ČÕČ«¹śŠĀŌöČ·Õļ²”ĄżŹżµÄĘ½¾łŹż£®
£Ø2£©¶Ō±ČĮ½·łĶ³¼ĘĶ¼ÖŠµÄŹż¾Ż£¬Ń”ŌńŅ»øö½Ē¶Č·ÖĪöĘĄ¼Ū“Ė“ĪŅßĒéæŲÖĘĒéæö£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
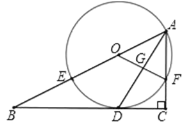
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬ADĘ½·Ö”ĻBAC½»BCÓŚµćD£¬OĪŖABÉĻŅ»µć£¬¾¹żµćA£¬DµÄ”ŃO·Ö±š½»AB£¬ACÓŚµćE£¬F£¬Į¬½ÓOF½»ADÓŚµćG£®
(1)ĒóÖ¤£ŗBCŹĒ”ŃOµÄĒŠĻߣ»
(2)ĒóÖ¤£ŗ![]() £»
£»
(3)ČōBE=8£¬sinB=![]() £¬ĒóADµÄ³¤£¬
£¬ĒóADµÄ³¤£¬
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ”Ī¢ĘóŅµĪŖ¼Óæģ²śŅµ×ŖŠĶÉż¼¶²½·„£¬Ņż½ųŅ»ÅśA£¬BĮ½ÖÖŠĶŗŵĻśĘ÷£®ŅŃÖŖŅ»ĢØAŠĶ»śĘ÷±ČŅ»ĢØBŠĶ»śĘ÷Ć抔Ź±¶ą¼Ó¹¤2øöĮć¼ž£¬ĒŅŅ»ĢØAŠĶ»śĘ÷¼Ó¹¤80øöĮć¼žÓėŅ»ĢØBŠĶ»śĘ÷¼Ó¹¤60øöĮć¼žĖłÓĆŹ±¼äĻąµČ£®
£Ø1£©ĆæĢØA£¬BĮ½ÖÖŠĶŗŵĻśĘ÷Ć抔Ź±·Ö±š¼Ó¹¤¶ąÉŁøöĮć¼ž£æ
£Ø2£©Čē¹ūøĆĘóŅµ¼Ę»®°²ÅÅA£¬BĮ½ÖÖŠĶŗŵĻśĘ÷¹²10ĢØŅ»Ęš¼Ó¹¤Ņ»ÅśøĆĮć¼ž£¬ĪŖĮĖČēĘŚĶź³ÉČĪĪń£¬ŅŖĒóĮ½ÖÖ»śĘ÷Ć抔Ź±¼Ó¹¤µÄĮć¼ž²»ÉŁÓŚ72¼ž£¬Ķ¬Ź±ĪŖĮĖ±£ÕĻ»śĘ÷µÄÕż³£ŌĖ×Ŗ£¬Į½ÖÖ»śĘ÷Ć抔Ź±¼Ó¹¤µÄĮć¼ž²»Äܳ¬¹ż76¼ž£¬ÄĒĆ“A£¬BĮ½ÖÖŠĶŗŵĻśĘ÷æÉŅŌø÷°²ÅŶąÉŁĢØ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ABCDĪŖĘ½ŠŠĖıߊĪ£¬AD=13£¬AB=25£¬”ĻDAB=¦Į£¬ĒŅcosa=![]() £¬µćEĪŖÖ±ĻßCDÉĻŅ»¶Æµć£¬½«Ļ߶ĪEAČʵćEÄꏱÕėŠż×Ŗ¦ĮµĆµ½Ļ߶ĪEF£¬Į¬½ÓCF£®
£¬µćEĪŖÖ±ĻßCDÉĻŅ»¶Æµć£¬½«Ļ߶ĪEAČʵćEÄꏱÕėŠż×Ŗ¦ĮµĆµ½Ļ߶ĪEF£¬Į¬½ÓCF£®
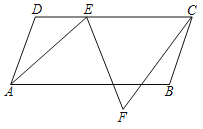
£Ø1£©ĒóĘ½ŠŠĖıߊĪABCDµÄĆ껿£»
£Ø2£©µ±µćC”¢B”¢FČżµć¹²Ļߏ±£¬ÉčEFÓėABĻą½»ÓŚµćG,ĒóĻ߶ĪBGµÄ³¤£»
£Ø3£©ĒóĻ߶ĪCFµÄ³¤¶ČµÄ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖÅ×ĪļĻßy£½x2+bx+c¹żA£¬B£¬CČżµć£¬µćAµÄ×ų±źŹĒ(3£¬0)£¬µćCµÄ×ų±źŹĒ(0£¬©3)£¬¶ÆµćPŌŚÅ×ĪļĻßÉĻ£®
£Ø1£©b£½”” ””£¬c£½”” ””£¬µćBµÄ×ų±źĪŖ”” ””£»
£Ø2£©ŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ”÷ACPŹĒŅŌACĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬Ēó³öĖłÓŠ·ūŗĻĢõ¼žµÄµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŹĒ·ń“ęŌŚµćPŹ¹µĆ”ĻPCA£½15”ć£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄŗį×ų±ź£®Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
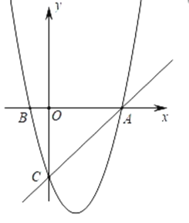
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬¶Ō½ĒĻßAC”¢BD½»ÓŚµćO£¬AB”ĪDC£¬AB£½BC£¬BDĘ½·Ö”ĻABC£¬¹żµćC×÷CE”ĶAB½»ABµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓOE£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪABCDŹĒĮāŠĪ£»
£Ø2£©ČōAB£½2![]() £¬BD£½4£¬ĒóOEµÄ³¤£®
£¬BD£½4£¬ĒóOEµÄ³¤£®
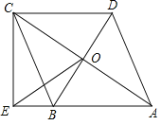
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ±ß³¤ĪŖ2µÄĮāŠĪABCDÖŠ£¬EŹĒ±ßADµÄÖŠµć£¬µćF”¢G”¢H·Ö±šŌŚ±ßAB”¢BC”¢CDÉĻ£¬ĒŅFG”ĶEF£¬EH”ĶEF£®
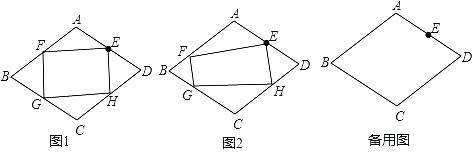
£Ø1£©ČēĶ¼1£¬µ±µć![]() ŹĒ±ß
ŹĒ±ß![]() ÖŠµćŹ±£¬ĒóÖ¤£ŗĖıߊĪ
ÖŠµćŹ±£¬ĒóÖ¤£ŗĖıߊĪ![]() ŹĒ¾ŲŠĪ£»
ŹĒ¾ŲŠĪ£»
£Ø2£©ČēĶ¼2£¬µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() Öµ£»
Öµ£»
£Ø3£©µ±![]() £¬ĒŅĖıߊĪ
£¬ĒŅĖıߊĪ![]() ŹĒ¾ŲŠĪŹ±£Øµć
ŹĒ¾ŲŠĪŹ±£Øµć![]() ²»Óė
²»Óė![]() ÖŠµćÖŲŗĻ£©£¬Ēó
ÖŠµćÖŲŗĻ£©£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com