
 如图,平面直角坐标系中,A(0,a)、B(b,0)、C(c,0),在B、C 两点各有一个平面镜,其中在B点的平面镜沿x轴方向,从P点发射两条光线PA、PB,反射光线BD经A点和反射光线CD相交.
如图,平面直角坐标系中,A(0,a)、B(b,0)、C(c,0),在B、C 两点各有一个平面镜,其中在B点的平面镜沿x轴方向,从P点发射两条光线PA、PB,反射光线BD经A点和反射光线CD相交.分析 (1)由偶次方及绝对值的非负性即可得出关于a、b、c的三元一次方程,解方程即可求出a、b、c的值,进而可得出点A、B、C的坐标,再根据三角形的面积公式即可求出△ABC的面积;
(2)根据对顶角相等结合三角形内角和为180°即可得出28°+∠PBA=38°+∠DCA,设∠DCA=x,∠NCH=y,则∠PBA=x+10°,再根据镜面反射性质结合三角形外角性质即可得出关于y的一元一次方程,解方程即可求出y的值,此题得解.
解答 解:(1)∵(2a+b-1)2+|b+c-1|=-(c-2)2,
∴$\left\{\begin{array}{l}{2a+b-2=0}\\{b+c-1=0}\\{c-2=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-1}\\{c=2}\end{array}\right.$,
∴A、B、C三点的坐标为A(0,$\frac{3}{2}$)、B(-1,0)、C(2,0).
∴S△ABC=$\frac{1}{2}$BC×AO=$\frac{1}{2}$(|-1|+2)×$\frac{3}{2}$=$\frac{9}{4}$;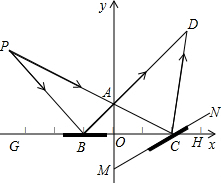
(2)∵∠PAB=∠DAC,
∴∠P+∠PBA=∠D+∠DCA,即:28°+∠PBA=38°+∠DCA,
设∠DCA=x,∠NCH=y,则∠PBA=x+10°,
由镜面反射性质可知:∠ABC=∠PBG=$\frac{1}{2}$(180°-∠PBA)=90°-$\frac{1}{2}$(x+10°),
∠DCN=∠PCM=$\frac{1}{2}$(180°-∠DCA)=90°-$\frac{1}{2}$x.
由三角形外角定理可知:∠DCH=∠DCN+∠NCH=∠ABC+∠D,
即:90°-$\frac{1}{2}$x+y=90°-$\frac{1}{2}$(x+10°)+38°,
解得:y=33°,
∴平面镜MN与x轴夹角的度数是33度.
点评 本题考查了坐标与图形性质、偶次方及绝对值的非负性、解三元一次方程组以及三角形的面积,本题属于基础题,难度不大,解题的关键是:(1)根据偶次方及绝对值的非负性得出关于a、b、c的三元一次方程;(2)根据镜面反射即角的计算找出关于y的一元一次方程.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
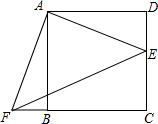 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在压力不变的情况下,某物体所承受的压强P(pa)与它的受力面积S(m2)之间的函数关系如图所示.
在压力不变的情况下,某物体所承受的压强P(pa)与它的受力面积S(m2)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
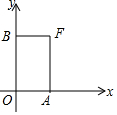 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAFB的周长与面积相等,则点F是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAFB的周长与面积相等,则点F是和谐点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com