
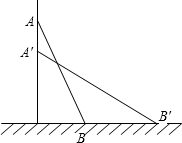
 一架梯子长2.5米,斜靠在一面垂直于地面的墙上,梯子底端离墙0.7米.
一架梯子长2.5米,斜靠在一面垂直于地面的墙上,梯子底端离墙0.7米.分析 (1)直接根据勾股定理即可得出结论;
(2)先根据勾股定理求出BC′的长,进而可得出结论.
解答  解:(1)∵△ABC是直角三角形,AB=2.5米,BC=0.7米,
解:(1)∵△ABC是直角三角形,AB=2.5米,BC=0.7米,
∴AC2=AB2-BC2=2.52-0.72=5.76,
∴AC=2.4(米).
答:这个梯子的顶端距地面有2.4米;
(2)∵梯子的顶端下滑了0.4米到A′,
∴A′C=2.4-0.4=2米.
∵△A′B′C是直角三角形,
∴B′C2=A′B′2-A′C2=2.52-22=2.25,
∴B′C=1.5米,
∴BB′=B′C-BC=1.5-0.7=0.8(米).
答:梯子的底端在水平方向滑动的距离BB′为0.8米.
点评 本题考查的是勾股定理的应用,解答本题的关键是两次运用勾股定理,注意掌握勾股定理的表达式.


科目:初中数学 来源: 题型:选择题
| A. | 0.8元/支,2.6元/本 | B. | 0.8元/支,3.6元/本 | ||
| C. | 1.2元/支,2.6元/本 | D. | 1.2元/支,3.6元/本 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
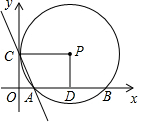 如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点.若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6.
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点.若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
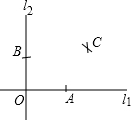 如图,在l1、l2上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于$\frac{1}{2}$AB长为半径作弧,两弧交于点C.若点C到l1、l2的距离分别为m-1,2n,则m与n的关系为( )
如图,在l1、l2上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于$\frac{1}{2}$AB长为半径作弧,两弧交于点C.若点C到l1、l2的距离分别为m-1,2n,则m与n的关系为( )| A. | m+2n=1 | B. | m-2n=1 | C. | 2n-m=1 | D. | n-2m=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
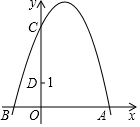 如图,抛物线y=-x2+bx+c与x轴交于A(3,0)、B(-1,0),与y轴交于点C,
如图,抛物线y=-x2+bx+c与x轴交于A(3,0)、B(-1,0),与y轴交于点C,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$和4 | B. | -$\frac{3}{5}$和5 | C. | $\frac{3}{5}$和5 | D. | $\frac{3}{5}$和4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com