练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、BC于D、E．若∠CAB=∠B+30°，CE=2cm．

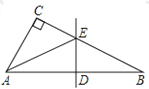
    求:（1）∠AEB 度数．

    （2）BC的长．

    【答案】见解析

    【解析】

    （1）根据DE垂直平分斜边AB，可得EA=EB，从而∠EAB=∠B，结合条件可求出∠CAE=30°，然后可求∠AEB 度数；

    （2）在△ACE中，∠C=90°,∠CAE=30°,所以AE=2CE=4,而AE=BE,BC=CE+BE=6．

    （1）解：∵DE垂直平分斜边AB

    ∴EA=EB

    ∴∠EAB=∠B

    ∵∠CAB=∠B+30°且∠CAB=∠CAE+∠EAB

    ∴∠CAE=30°

    ∴∠AEB=∠CAE+∠C=30°+90°=120°

    （2）在△ACE中，

    ∵∠C=90°,∠CAE=30°,

    ∴AE=2CE=4,

    又∵AE=BE,

    ∴BC=CE+BE=6cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，EA⊥AB，BC⊥AB，AB=AE=2BC，D为AB中点，在“①DE=AC；②DE⊥AC；③∠EAF=∠ADE；④∠CAB=30°”这四个结论中，正确的个数有 （ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D是BC的中点，作射线AD，在线段AD及其延长线上分别取点E，F，连结CE，BF.添加一个条件，使得△BDF≌△CDE,你添加的条件是_____________________（不添加辅助线）.

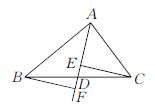
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在锐角三角形ABC中，直线l为BC的中垂线，射线m为∠ABC的角平分线，直线l与m相交于点P.若∠BAC＝60°，∠ACP＝24°，则∠ABP的度数是( )

    A. 24° B. 30° C. 32° D. 36°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，点D、E、F分别在AB、BC、AC边 且BE＝CF，AD+EC＝AB．

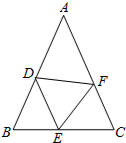
    （1）求证：△DEF是等腰三角形；

    （2）当∠A＝40°时，求∠DEF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，中，∠BAC=90°，AB=AC，F是BC上一点，BDAF的延长线与D，CEAF于E，已知CE=5，BD=2，ED=__________

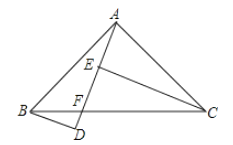
    查看答案和解析>>

    科目：初中数学 来源： 题型：

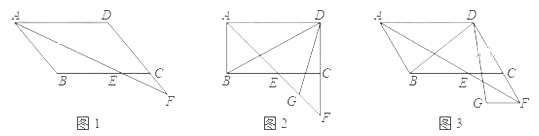
    【题目】在平行四边形ABCD中，E是BC上任意一点，延长AE交DC的延长线与点F.

    (1)在图中当CE=CF时，求证：AF是∠BAD的平分线.

    (2)在（1）的条件下，若∠ABC=90°，G是EF的中点（如图），请求出∠BDG的度数.

    (3)如图,在（1）的条件下，若∠BAD=60°,且FG∥CE,FG=CE,连接DB、DG,求出∠BDG的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

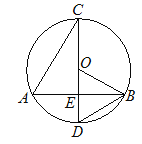
    【题目】如图，CD为⊙O的直径，弦AB交CD于点E，连接BD、OB．

    （1）求证：△AEC∽△DEB；

    （2）若CD⊥AB，AB＝8，DE＝2，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与轴交于，两点，交轴于点．

    求抛物线的解析式；

    点是第二象限内一点，过点作轴交抛物线于点，过点作轴于点，连接、，若．求的值并直接写出的取值范围（利用图完成你的探究）．

    如图，点是线段上一动点（不包括点、），轴交抛物线于点，，交直线于点，设点的横坐标为，求的周长．

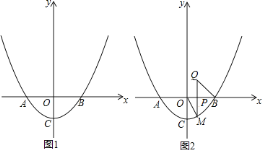
    查看答案和解析>>

    同步练习册答案