
分析 根据黄金分割点的定义,知较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$倍,可得BC的长,同理求得AC′的长,则CC′即可求得.
解答  解:∵线段AB=a,C、C′是线段AB的两个黄金分割点,
解:∵线段AB=a,C、C′是线段AB的两个黄金分割点,
∴较小线段AC′=BC=$\frac{3-\sqrt{5}}{2}$a,
则CC′=AB-AC′-BC=a-2×$\frac{3-\sqrt{5}}{2}$a=($\sqrt{5}$-2)a.
故答案是:($\sqrt{5}$-2)a.
点评 本题考查了黄金分割,应该识记黄金分割的公式:较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$倍,较长的线段=原线段的$\frac{\sqrt{5}-1}{2}$倍.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:解答题
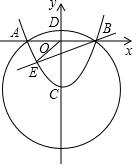 如图,抛物线y=ax2-4与x轴相交于A(-3,0)、B,与y轴相交于点C.以点C为圆心,CA长为半径画⊙C,⊙C与y轴的正半轴相交于点D.
如图,抛物线y=ax2-4与x轴相交于A(-3,0)、B,与y轴相交于点C.以点C为圆心,CA长为半径画⊙C,⊙C与y轴的正半轴相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{6}$ | D. | $\sqrt{0.01}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 定价(元) | 100 | 110 | 120 | 130 | 140 | 150 |
| 销量(个) | 80 | 100 | 110 | 100 | 80 | 60 |
| A. | 定价是常量,销量是变量 | |
| B. | 定价是变量,销量是不变量 | |
| C. | 定价与销售量都是变量,定价是自变量,销量是因变量 | |
| D. | 定价与销量都是变量,销量是自变量,定价是因变量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一石头,石头终将落地 | B. | 从装有黑球,白球的袋里摸出红球 | ||
| C. | 太阳绕着地球转 | D. | 买1张彩票,中500万大奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com