
分析 根据xy≠0可以在等式的两边同时除以y2得到:($\frac{x}{y}$)2-3×$\frac{x}{y}$-2=0,故设$\frac{x}{y}$=t,原方程转化为关于t的方程,通过解该方程可以求得$\frac{x}{y}$的值.
解答 解:∵xy≠0,
∴由原方程,得
($\frac{x}{y}$)2-3×$\frac{x}{y}$-2=0,故设$\frac{x}{y}$=t,
则t2-3t-2=0,
解得t=$\frac{3±\sqrt{17}}{2}$
∴$\frac{x}{y}$=$\frac{3±\sqrt{17}}{2}$.
故答案是:$\frac{3±\sqrt{17}}{2}$.
点评 本题主要考查换元法在解一元二次方程中的应用.换元法是借助引进辅助元素,将问题进行转化的一种解题方法.这种方法在解题过程中,把某个式子看作一个整体,用一个字母去代表它,实行等量替换.这样做,常能使问题化繁为简,化难为易,形象直观.


科目:初中数学 来源: 题型:解答题
 我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠ABC=90°,DE⊥AE于点E,CF∥ED,连接EF交CD边于点G,试判断∠EAB与∠FCB有怎样的数量关系,写出你的猜想,并加以证明.
如图,在四边形ABCD中,∠ABC=90°,DE⊥AE于点E,CF∥ED,连接EF交CD边于点G,试判断∠EAB与∠FCB有怎样的数量关系,写出你的猜想,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
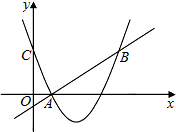 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com